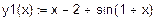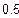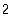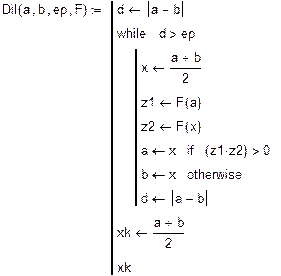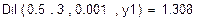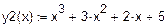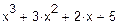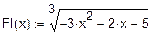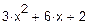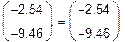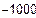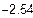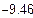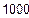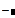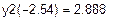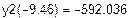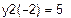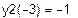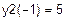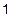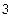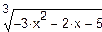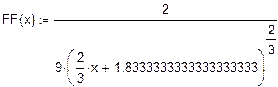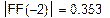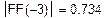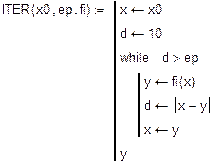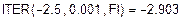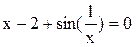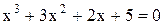Завдання на виконання роботи. Мета роботи- ознайомитись з методами знаходження коренів нелінійних алгебраїчних рівнянь у розв'язанні задач моделювання

КАБІНЕТ МІНІСТРІВ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ БІОТЕХНОЛОГІЙ І ПРИРОДОКОРИСТУВАННЯ УКРАЇНИ

Лабораторна робота 1

РОЗВ'ЯЗАННЯ ЗАДАЧ ПО МОДЕЛЮВАННЮ ТЕХНОЛОГІЧНИХ

ОБ'ЄКТІВ КЕРУВАННЯ З ВИКОРИСТАННЯМ МЕТОДІВ ЗНАХОДЖЕННЯ КОРЕНІВ НЕЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ

Виконав

Нестерук А.О

Київ 2008

Мета роботи - ознайомитись з методами знаходження коренів нелінійних алгебраїчних рівнянь у розв'язанні задач моделювання. Навчитись графічно і аналітично відокремлювати корені рівнянь і уточнювати їхні значення за допомогою числових методів з використанням ППП Mathcad.

Завдання на виконання роботи

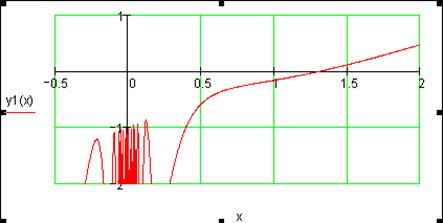
Графічним методом відокремити корені одного із нелінійних алгебраїчних рівнянь завдання і знайти один із коренів методом дихотомії (діленням відрізка навпіл). Корені іншого рівняння відокремити аналітично і знайти один із коренів методом ітерацій. Значення коренів визначити з точністю до 0, 0001. Накреслити графік для відокремлення кореня і скласти програми уточнення коренів у середовищі Mathcad.

Висновок

Під час лабораторної роботи, ми ознайомились з методами знаходження коренів нелінійних алгебраїчних рівнянь у розв'язанні задач моделювання. Навчилась графічно і аналітично відокремлювати корені рівнянь і уточнювати їхні значення за допомогою числових методів з використанням ППП Mathcad.Графічне відокремлення кореня виконується побудовою графіка функції рівняння і знаходженням точки перетину функції з віссю ОХ. Інтервал вибирається довільно з урахуванням умови зміни знака функції на кінцях інтервалу і монотонності функції на інтервалі. Якщо рівняння можна представити у вигляді двох простих функцій, то будуються їхні графіки і знаходяться точки перетину цих графіків. Координати точок перетину і будуть коренями рівняння. Відносно їх вибираються інтервали, на яких знаходять точніші значення коренів.

Уточнення коренів виконується із заданою наперед точністю методами дихотомії (ділення відрізка навпіл), ітерацій, Ньютона.