
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Простые проценты
|
|
В зависимости от способа начисления проценты делят на простые и сложные. При использовании простых процентов сумма процентов в течение всего срока долга определяется исходя из первоначальной суммы долга независимо от количества периодов начисления и их длительности. Сумма процентов при этом определяется по формуле:
J = n • Jr = n • i• P, (2.3)
Jr - сумма процентов за год,
Р - сумма, на которую начисляются проценты;
i – годовая ставка процентов в относительных единицах.
Если срок хранения вклада выражается в днях, то в формулу (2.3) следует подставить выражение n = t / К.
Сумма долга с начисленными процентами будет определять выражением:
S = P + J = P(1 + n • i) (2.4)
Эта формула может быть представлена в виде:
S = P • kн (2.5)
где kн - множитель (коэффициент) наращения.
Заметим, что увеличение процентной ставки или срока в (k) раз увеличит множитель наращения в (1 + kni)/(l + ni) раз.
В банковской практике различных стран срок в днях и расчетное количество дней в году при начислении процентов определяется по-разному.
В так называемой германской (коммерческой) практике расчёт числа дней основывается на длительности года в 360 дней и месяцев в 30 дней; во французской - длительность года равна 360 дням, а количество дней в месяцах - равно их фактической календарной длительности (28, 29, 30, 31); в английской - длительность года равна 365 дням и соответствующая точная длительность месяцев.
При изменении суммы на счёте общая сумма процентов за весь срок хранения вклада будет равна сумме процентов, начисленных для каждого периода начисления, в котором сумма на счёте была постоянна. При этом в практике используется также методика расчета с вычислением так называемых процентных чисел, определяемых выражением:
Процентное число = (Сумма • Длительность в днях) / 100.
Для определения суммы начисленных процентов все процентные числа складываются и их сумма делится на постоянный делитель, вычисляемый следующим образом:
Постоянный делитель = Количество дней в году / Годовая ставка процентов.
Объединяя данные выражения, получаем для одного период начисления:
Проценты = (Сумма • Длительность в днях• Процентная ставка)/(100 • Количество дней в году) = Длительность в днях / Количество дней в году • Процентная ставка • Сумма /100.
Если ставки процентов изменяются в течении срока хранения вклада, сумму начисленных процентов можно определить, прим последовательно формулу (2.3).
Пусть на последовательных интервалах времени n1 и n2 используются простые ставки процентов i1 и i2, тогда по формуле (2.3) сумма процентов, начисленных за первый интервал, будет равна:
J1 =n1 • i1 • Р.
Сумма процентов, начисленных за второй интервал, составит:
J2 =n2 • i2 • Р.
Общая сумма процентов за два интервала начисления будет равна:
J = J1 + J2 = n1 • i1 • Р + n2 • i2 • Р = P(n1 • i1 + n2 • i2)
Наращенная сумма за два интервала начисления составит:
S = P + J = Р(n1 • i1 + n2 • i2).
При N интервалах начисления, на каждом из которых будет применяться своя ставка процентов, сумма процентов составит:
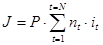 (2.6)
(2.6)
Сумма вклада с процентами (наращенная сумма) будет в этом случае равна:
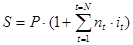 (2.7)
(2.7)
Из формулы (2.4.) можно при прочих заданных условиях определить срок вклада в годах:
n = (S - P)/P • i (2.8)
или в днях:
t = ((S - P)/P • i)K, (2.9)
а также ставку простых процентов при прочих заданных условиях:
i = (S - P)/(P • t)K. (2.10)
Используя формулу (2.4.), можно определить сумму вклада при заданных значениях суммы вклада с начисленными процентами, срока вклада и ставки процентов:
P = S/(1 + n • i) = S/(1 + i •t/k). (2.11)
Это выражение можно также записать в виде:
P = S • kd,
где kd =  - коэффициент дисконтирования (он, как видим величина множителя (коэффициента) наращения).
- коэффициент дисконтирования (он, как видим величина множителя (коэффициента) наращения).