
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сложные проценты
|
|
При начислении сложных процентов сумма процентов, начисленных после первого периода начисления, являющегося частью общего срока хранения вклада, не выплачивается, а присоединяется сумме вклада. База для начисления сложных процентов в отличие от использования простых процентов будет увеличиваться с каждым периодом начисления, являющимся частью общего срока хранения вклада.
Если проценты за период начисления начисляются по постоянной сложной старке in и все периоды начисления имеют одинаковую длительность, сумма вклада с процентами в конце первого периода по формуле (2.4) будет равна:
S1=Р • (1+n • i).
Сумма вклада с процентами в конце второго периода составит:
S2=S1 • (1+n • in)=Р • (1+n • i)2
Если в течение срока хранения вклада будет N одинаковых периодов начисления, сумма вклада с процентами в конце срока составит:
S=Р • (1+ i)n. (2.12)
Сумма начисленных процентов будет равна:
J = S-P=P[(1 + n • i)N - 1]. (2.13)
Если срок хранения вклада в годах (n) не является целым числом, множитель наращения можно определить двумя способами. При первом способе используют формулу (2.12) с соответствующим нецелым показателем степени. При втором способе множитель наращения определяется по выражению:
kh = (1+ i)n1 - (1+n2 • i), (2.14)
где n1 - целое число лет в течение срока вклада;
n2 - оставшаяся дробная часть года.
При начислении сложных процентов несколько раз в году (месяцам, по кварталам, по полугодиям) сумма вклада с процента (наращенная сумма) при сроке (т) лет будет равна:
S=P(1 + n • i)N= P(1 + j/m)N (2.15)
где in - ставка за период начисления;
j - номинальная годовая ставка процентов;
m - количество периодов начисления в году;
N - количество периодов начисления в течение срока хранения вклада (N = n • m).
Сумма начисленных процентов составит:
J = P[(l+j/m)N – 1 ]. (2.16)
Используя формулы для наращенной суммы при начислении сложных процентов один или несколько раз в году, можно получить выражение для срока хранения вклада при заданных прочих условиях. При использовании сложной годовой ставки процентов срок хранения в годах будет равен:
n = 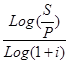 (2.17)
(2.17)
Из формул для наращенной суммы можно также определить ставку сложных процентов при прочих заданных условиях:
i= 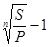 (2.18)
(2.18)
При использовании годовой ставки сложных процентов(1) и сроке хранения (n) лет дисконтированное значение будущей суммы вклада с процентами будет равно:
P = S/(l+i)n=S • kd, (2.19)
где kd = 1/(1 + i)n - коэффициент дисконтирования (приведения).
При наличии сложных процентов несколько раз в году дисконтированная сумма будет равна:
P=S/(1+j/m)N. (2.20)