Начисление процентов при регулярных взносах

Если ежегодно в конце каждого года в течении (n) лет на депозитный счёт будет поступать сумма (R), а проценты начисляться сложной ставке (i), суммы последовательных взносов с процентам начисленными на момент окончания срока хранения депозит формуле (2.12) будут равны:

S₁ = R(l + i)^n-1,

S₂ = R(l + i)^n-2,

S_n-1 = R(l + i),

S_n = R/

Применив к сумме всех значений St (t = 1, 2,..., n) формулу для суммы

S= 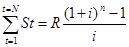(2.23)

Последовательность денежных поступлений, осуществляемых равными суммами через равные периоды времени, называют «потоком постнумерандо» или постоянной финансовой рентой.

Если взносы в размере (R) будут вноситься (р) раз в году в конце расчётных периодов и на суммы на счёте (т) раз в год будут начисляться сложные проценты по номинальной годовой ставке (j), выражение для суммы всех взносов с начисленными процентами на (n) лет будет иметь следующий вид:

S = 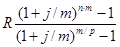. (2.24)

Из формул (2.23) и (2.24) можно определить размер взносов при прочих заданных условиях:

R= 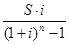, (2.25)

или

R= 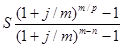. (2.26)

Если одинаковые суммы R, будут поступать на депозитный счёт в начале каждого года (это есть «поток пренумерандо»), то сумма всех поступлений с начисленными процентами через n лет будет равна:

S = 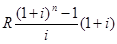. (2.27)

Если взносы в размере R будут вноситься на депозитный счёт (р) раз в году в начале каждого расчётного периода и на них (m) раз в год будут начисляться сложные проценты по номинальной годовой став (j), сумма всех взносов с начисленными процентами через (n) лет будет равна:

S = 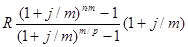. (2.28)

Из формулы (2.27) и (2.28) можно определить размер взносов и прочих заданных условиях:

R= 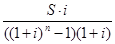(2.29)

или

R= 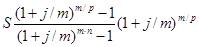(2.30)

2.3.5. Расчёты в условиях инфляции

В современных российских условиях одним из подходов к учёту инфляции может быть определение её роста в соответствии с ростом курса доллара США. В общем же случае при количественной оценке используют уровень и индекс инфляции.

Уровень инфляции показывает, на сколько процентов выросли цены за рассматриваемый период времени, и его можно записать так;

r = 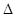S/S 100

или

r = 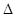S/S,

где 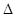S - сумма, на которую надо увеличить сумму

S для сокращения её покупательной способности.

Сумма, покупательная способность которой с учётом инфляции должна соответствовать покупательной способности суммы S, будет равна:

Sr = S + 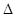S = S + rS-S(1 +г) (2.31)

или

S = S J_n, (2.32)

где J_n - индекс инфляции, определяемой соотношением

J = J + r. (2.33)

Индекс инфляции показывает, во сколько раз выросли цены за рассматриваемый период времени.

Если необходимо определить уровень инфляции за некоторый срок (например год) на основании значений уровня инфляции за периоды, которые меньше этого срока (например месяцы), для первого такого периода можно записать соотношение:

S_r1=S(1+r₁)

для следующего:

S₂=S₁(1+r₂)=S(1+r₁)(1+r₂)

Индекс инфляции за рассмотренный срок будет равен:

J_n=(1+r₁)(1+r₂)(1+r₃) … (1+r_n) (2.34)

где n – количество периодов.

При равных периодах и равных уровнях инфляции за к период формула (2.34) принимает вид:

J_n = (l+r_n)ⁿ (2.35)

Уровень инфляции за весь срок в соответствии с форм (2.35) будет равен:

R=Jn – 1 (2.36)

Из формулы (2.32) следует, что сумма S, соответствующая сумме Sr и характеризующая реальное значение будущей суммы с учетом инфляции за рассматриваемый срок, будет равна:

S = S_r/j_n.

Следовательно, сумма депозита с процентами, пересчитанная (приведённая) на момент его оформления с учётом уровня инфляции за период хранения, будет равна:

для ставки простых процентов

P_r=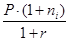

для ставки сложных процентов при их начислении один раз в году

P_r=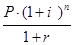

для ставки сложных процентов при их начислении несколько раз в году

P_r=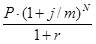

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

К ТЕМЕ 2 «УПРАВЛЕНИЕ АКТИВАМИ И ОБЯЗАТЕЛЬСТВАМИ БАНКА»

2.1. Размещение привлечённых и собственных средств.

Определение дохода финансовых операций