Свойства определенного интеграла.

Будем предполагать, что все рассматриваемые ниже функции интегрируемы на заданных промежутках.

Свойство 1. (6)

Для доказательства составим интегральные суммы (3) в обоих случаях с теми же точками деления. Они будут отличаться только знаком за счет знаков 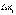: слева > 0, справа 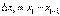< 0. Значит, в пределе получится нужное равенство.

Свойство 2. 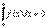(7)

В этом случае отрезок интегрирования равен нулю и интегральная сумма – тоже.

Свойство 3. Постоянный множитель можно выносить за знак определенного интеграла: если , то

(8)

Доказательство:

(см.(4)) = = =

Свойство 4. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от этих функций: (9)

Свойство 5. Если отрезок [a, b] разбит точкой с на две части [a, c] и [c, b], то (10)

Доказательство. Составим интегральную сумму для на [a, b]. Так как предел этих сумм не зависит от способа разбиения [a, b] на части, то рассмотрим только те разбиения, в которых точка с входит в качестве точки деления. Тогда , где - суммы, соответствующие отрезкам [a, c] и [c, b]. Переходя в последнем равенстве к пределу при , получим соотношение (10).

Замечание. Свойство сохраняется при любом взаимном расположении точек a, b, c. На рисунке 2. дана геометрическая иллюстрация свойства 5 для случая, когда и a < c < b: площадь трапеции aABb равна сумме площадей трапеций aACc и cCBb.

Свойство 6. Если всюду на отрезке [a, b] функция неотрицательна то а если то

Доказательство. В самом деле, любая интегральная сумма для на [a, b] неотрицательна, так как Переходя к пределу в неравенстве , получаем

Для случая на [a, b] доказательство аналогичное.

Геометрический смысл утверждения очевиден.

Следствие из свойств 5 и 6.

Интегрирование в симметричных пределах можно упростить, если воспользоваться формулами:

a) , если - четная функция,

б) , если - нечетная функция.

Эти утверждения наглядно иллюстрируются геометрически (рис. 3).

Свойство 7. (Интегрирование неравенств).

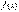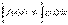Если на отрезке [a, b] функции и удовлетворяют условию , то (11).

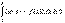Доказательство. На отрезке [a, b] разность , тогда по свойству 6: Применим затем свойство 4: Отсюда следует неравенство (11).

Если > 0 и > 0 на [a, b], то свойство 7 иллюстрируется геометрически (рис. 4). Так как , то площадь криволинейной трапеции не больше площади .

Свойство 8. (Оценка определенного интеграла). Если на отрезке [a, b] функция удовлетворяет условию , то определенный интеграл удовлетворяет неравенству (12)