Основное Определение.

Пусть некоторая функция задана при 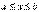. Разобьем этот интервал на произвольных частей точками и составим сумму, которая называется интегральной суммой для функции на отрезке [ 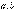]: (3)

где , а каждая точка произвольно выбрана между и .

Определение 2. Функция , для которой на отрезке [a, b] существует определенный интеграл, называется интегрируемой на этом отрезке.

Естественно возникает вопрос: при каких условиях функция , определенная на [a, b], интегрируема на этом отрезке? Не приводя доказательств, рассмотрим эти условия.

Теорема 1. Если функция непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

Сформулируем и более общую теорему об интегрируемости.

Теорема 2. Если функция ограничена на [a, b] и непрерывна на нем всюду, кроме конечного числа точек, то она интегрируема на этом отрезке.