Вычисление определенного интеграла. Формула Ньютона - Лейбница.

Теорема. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленных для для верхнего и нижнего пределов интегрирования: . (17)

Доказательство. Пусть есть некоторая первообразная для функции на отрезке [a, b].

С другой стороны, в установлено, что одной из первообразных для на отрезке [a, b] является функция так как для нее справедливо равенство (16). Известно, что две любые первообразные от данной функции отличаются друг от друга на постоянное слагаемое С: ,

(18)

При соответствующем выборе С равенство (18) справедливо при всех значениях . Подставим в него значение : . Следовательно, для любого значения

Полагая в последнем равенстве , получим .

Заменим переменную на более привычную 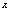. Разность принято условно записывать в виде .

Формула выражающая определенный интеграл от непрерывной функции через неопределенный, называется формулой Ньютона –Лейбница.

Формула (17) дает простой и удобный метод вычисления определенного интеграла от непрерывной функции, если известна первообразная подынтегральной функции. Только с появлением этой формулы определенный интеграл смог занять в математике то важное место, какое он занимает в настоящее время.