Доказательство.

По свойству функций, непрерывных на отрезке 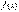достигает своего наименьшего и наибольшего значений и принимает все промежуточные значения между и : 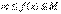. В силу формулы (12), предположив, что a< b, имеем

Обозначим тогда По свойству непрерывных функций найдется значение такое, что ,

Следовательно, из равенства (14) получим нужное соотношение (13).

Замечание. В выражении (14) называют средним (средним интегральным) значением функции 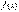на отрезке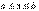

Геометрический смысл среднего значения показан на рис. 6. Значение должно быть таким, чтобы площадь прямоугольника равнялась площади криволинейной трапеции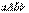

Заметим, что теорема говорит о существовании точки , но не дает способа ее нахождения.

Свойство 10. Абсолютное значение интеграла не превосходит интеграла от абсолютного значения функции: