Решение невырожденных линейных систем. Формулы Крамера.

невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом либо по формулам Крамера: .

Матричный способ:

Пусть дана система n линейных уравнений с n неизвестными

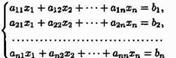
или в матричной форме А*Х=В. Основная матрица А такой системы квадратная. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.

Найдем решение данной системы уравнений в случае D¹ 0.. Умножив обе части уравнения А*Х=В слева на матрицу A^-1, получим A^-1*A*X=A^-1*B Поскольку. A^-1*A=E и Е*Х=Х, то X=A^-1*B

то есть

Отсюда следует, что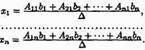

Но 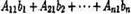есть разложение определителя

по элементам первого столбца. Определитель D₁ получается из определителя D путем замены первого столбца коэффициентов столбцом из свободных членов. Итак,

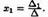Аналогично: ,

где D2 получен из D путем замены второго столбца коэффициентов столбцом из свободных членов: ,...,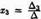

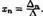
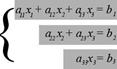25.Решение систем линейных уравнений методом Гаусса.

Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов казалась трапециевидной или близкой к трапециевидной.

При решении методом Гаусса систем линейных уравнений с любым числом уравнений и неизвестных в системе уравнений и в расширенной матрице системы можно:

1.переставлять местами строки (это и было упомянуто в самом начале этой статьи);

2.если в результате других преобразований появились равные или пропорциональные строки, их можно удалить, кроме одной;

3.удалять " нулевые" строки, где все коэффициенты равны нулю;

4.любую строку умножать или делить на некоторое число;

5.к любой строке прибавлять другую строку, умноженное на некоторое число.

Пусть дана система линейных уравнений.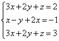

Для упрощения решения составим расширенную матрицу системы: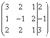

Для удобства деления коэффициентов при переменных переставим местами первую и вторую строки матрицы системы: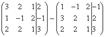

С помощью нового первого уравнения исключим переменную x из второго и всех последующих уравнений. Для этого ко второй строке матрицы прибавим первую, умноженную на 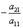(в нашем случае на 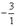), к третьей – первую строку, умноженную на 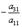(в нашем случае на 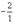). Это возможно, так как

В результате получим матрицу эквивалентную данной системе новой системы уравнений, в которой все уравнения, начиная со второго не содержат переменнную x:

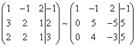
Для упрощения второй строки полученной системы умножим её на и получим вновь матрицу системы уравнений, эквивалентной данной системе:

Теперь, сохраняя первое уравнение полученной системы без изменений, с помощью второго уравнения исключаем переменную y из всех последующих уравнений. Для этого к третьей строке матрицы системы прибавим вторую, умноженную на 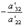(в нашем случае на 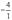). В результате вновь получим матрицу системы, эквивалентной данной системе линейных уравнений: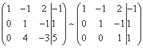

Мы получили эквивалентную данной трапециевидную систему линейных уравнений: