Линейные операции над векторами. Проекция вектора на ось, разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы. Действия над векторами.

Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число. Сложение векторов и осуществляется по правилу треугольника.

Для сложения векторов применяется также правило параллелограмма.

Вектор называется противоположным вектором к вектору , если он коллинеарен вектору , равен ему по длине, но направлен в противоположную сторону вектору .

Проекция вектора на ось – это вектор, началом и концом которого являются соответственно проекции начала и конца заданного вектора.

Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.

Найдем скалярное произведение этих векторов

a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11; Найдем модуль вектора |b| = √ 3² + 4² = √ 9 + 16 = √ 25 = 5

Найдем проекцию вектора a на вектор b

Ответ: Пр _ba = 2.2.

Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.

Найдем скалярное произведение этих векторов: a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 1

Найдем модуль вектора b |b|=√ 4²+2²+4²=√ 16+4+16=√ 36=6

Найдем проекцию вектора a на вектор b

Ответ: Пр _ba = 2

Проекции вектора на оси координат называются его координатами. В этом заключается их геометрический смысл.

Если задана система координат на плоскости и в пространстве, то начало вектора можно всегда совместить с началом координат, не меняя при этом длину и направление. Выделим на координатных осях единичные векторы и обозначим .Выберем произвольный вектор 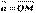. Найдем проекции вектора на координатные оси.

Проведем через конец вектора плоскости, параллельные координатным плоскостям. Точки пересечения с осями обозначим соответственно через М₁, М₂, М₃. Получили прямоугольный параллелепипед, одной диагональю которого является.

Тогда ; ; . По определению суммы получим, что , но т.к. , то . Но , ,

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом. Модуль вектора можно найти, если мы знаем его проекции на координатные оси. На плоскости задан вектор а. Опустим с начала и конца вектора перпендикуляры на координатные оси для нахождения его проекций. В соответствии с теоремой Пифагора 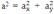. Отсюда

Чтобы найти модуль вектора надо извлечь корень квадратный из суммы квадратов его проекций. Для вектора, если он задан на плоскости, а_x = х_к − х_н, а_y = y_к − y_н. Следовательно, модуль вектора можно найти по формуле .

Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Направляющие косинусы однозначно задают направление вектора.

Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

Соответственно координатам единичного вектора равны его направляющим косинусам. Сумма квадратов направляющих косинусов равна единице.