
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Необходимое и достаточное условия возрастания и убывания функций. Необходимое условие экстремума. Первое и второе достаточные условия экстремума.
|
|
ОПРЕДЕЛЕНИЕ. Функция  называется возрастающей (неубывающей) на интервале
называется возрастающей (неубывающей) на интервале  если для любых
если для любых  таких, что
таких, что  значения функции
значения функции  и
и 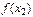 удовлетворяют неравенству
удовлетворяют неравенству 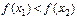
( ).
).
Функция  называется убывающей (невозрастающей) на интервале
называется убывающей (невозрастающей) на интервале  если для любых
если для любых  таких, что
таких, что  значения функции
значения функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству 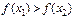 (
( ).
).
Интервалы возрастания и убывания функции называются интервалами монотонности функции.
Из определения возрастающей функции следует, что если 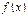 возрастает на
возрастает на  , то на этом интервале приращение аргумента
, то на этом интервале приращение аргумента  и соответствующее ему приращение функции
и соответствующее ему приращение функции 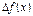 будут иметь одинаковый знак.
будут иметь одинаковый знак.
Действительно, если 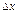
 , то
, то 
⇒  ,
,
⇒ 
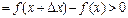 .
.
Если 
 , то
, то 
⇒ 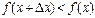 ,
,
⇒ 
 .
.
Аналогично показывается, что если  убывает на
убывает на  , то на этом интервале приращение аргумента
, то на этом интервале приращение аргумента  и соответствующее ему приращение функции
и соответствующее ему приращение функции  будут иметь разный знак.
будут иметь разный знак.
Справедлива следующая теорема. Иначе говоря, функция  называется возрастающей на интервале
называется возрастающей на интервале  , если большему значению аргумента из этого интервала соответствует большее значение функции.
, если большему значению аргумента из этого интервала соответствует большее значение функции.
Иначе говоря, функция  называется убывающей на интервале
называется убывающей на интервале  , если большему значению аргумента из этого интервала соответствует меньшее значение функции.
, если большему значению аргумента из этого интервала соответствует меньшее значение функции.
ТЕОРЕМА 1 (необходимое и достаточное условия возрастания (убывания) функции). Пусть функция  дифференцируема на интервале
дифференцируема на интервале  . Тогда
. Тогда
1) если функция  возрастает (убывает) на
возрастает (убывает) на  , то на этом интервале ее производная неотрицательна (неположительна), т.е.
, то на этом интервале ее производная неотрицательна (неположительна), т.е.  ,
, 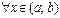
( ,
,  );
);
2) если производная  на интервале
на интервале  положительна (отрицательна), т.е.
положительна (отрицательна), т.е.  ,
, 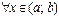 (
( ,
, 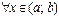 ),
),
то функция  на
на  возрастает (убывает).
возрастает (убывает).
Доказательство: 1) (Необходимость.) Пусть  возрастает на
возрастает на  . Требуется доказать, что
. Требуется доказать, что  ,
,  .
.
Так как  возрастает на
возрастает на  , то знак
, то знак  и соответствующего ему приращения
и соответствующего ему приращения  совпадают.
совпадают.
⇒  ,
, 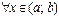 ,
,  (при условии, что
(при условии, что  ).
).
Но тогда  .
.
Аналогично доказывается, что если 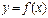 убывает на
убывает на  , то
, то  ,
, 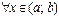 .
.
2) (Достаточность.) Пусть 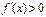 ,
,  . Требуется доказать, что
. Требуется доказать, что  возрастает на
возрастает на  .Пусть
.Пусть  ,
,  . Рассмотрим разность
. Рассмотрим разность  . По теореме Лагранжа, существует точка
. По теореме Лагранжа, существует точка 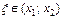 , такая, что
, такая, что  .
.
⇒  .
.
Так как  и
и 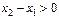 получаем:
получаем:  ,
, 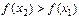 .
.
Следовательно, 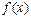 возрастает на интервале
возрастает на интервале  .
.
Аналогично доказывается, что если 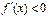 ,
,  , то
, то  убывает на
убывает на  .
.
 12. Выпуклость функции, точки перегиба
12. Выпуклость функции, точки перегиба
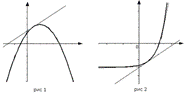
График функции  , дифференцируемой на интервале
, дифференцируемой на интервале  , является на этом интервале выпуклым, если график этой функции в пределах интервала
, является на этом интервале выпуклым, если график этой функции в пределах интервала  лежит не выше любой своей касательной (рис. 1).
лежит не выше любой своей касательной (рис. 1).
График функции 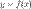 , дифференцируемой на интервале
, дифференцируемой на интервале 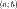 , является на этом интервале вогнутым, если график этой функции в пределах интервала
, является на этом интервале вогнутым, если график этой функции в пределах интервала  лежит не ниже любой своей касательной (рис. 2).
лежит не ниже любой своей касательной (рис. 2).