Основные свойства бесконечно малых функций

1) Сумма конечного числа б.м функций является функцией б.м.

2) Произведение б.м функции на ограниченную есть функция б.м.

3) Произведение двух б.м функций есть функция б.м.

4) Произведение б.м функции на константу является б.м функцией.

5) Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.

6) Функция , обратная к б.м функции , есть функция бесконечно большая. Верно и обратное.

БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х₀, наз. бесконечно большой функцией при х, стремящемся к x₀, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х₀ и таких, что |х - х₀ | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:

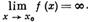Аналогичным образом определяются

Напр., означает, что для любого М> 0 найдется такое δ =δ (M)> 0, что для всех z< -δ выполняется неравенство f(x)> M.

5.Непрерывность функции: непрерывность функции в точке, в интервале и на отрезке, точки разрыва функции и их классификация, основные теоремы о непрерывных функциях, непрерывность элементарных функций.

Функция называется непрерывной в точке , если:

1. функция определена в точке и ее окрестности;

2. существует конечный предел функции в точке ;

3. это предел равен значению функции в точке , т.е.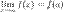

4. При нахождении предела функции , которая является непрерывной, можно переходить к пределу под знаком функции, то есть

Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.

Функция называется непрерывной справа в точке , если .

Функция называется непрерывной слева в точке , если .

Функция называется непрерывной в интервале , если она непрерывна в каждой точке этого интервала.

Функция называется непрерывной на отрезке , если она является непрерывной в интервале , непрерывной справа в точке , то есть и непрерывной слева в точке , то есть 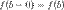. Свойства функций непрерывных на отрезке:

1. Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.

2.Непрерывная на отрезке 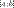функция является ограниченной на этом отрезке.

3. Теорема Больцано-Коши. Если функция 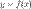является непрерывной на отрезке и принимает на концах этого отрезка неравные между собой значения, то есть , , то на этом отрезке функция принимает и все промежуточные значения между и .

4.Если функция , которая непрерывна на некотором отрезке , принимает на концах отрезка значения разных знаков, то существует такая точка такая, что

Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1.функция определена в точке и ее окрестности;

2.существует конечный предел функции в точке ;

3.это предел равен значению функции в точке , т.е.

называется точкой разрыва функции.

Точка разрыва первого рода. Если в точке существуют конечные пределы 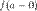и , такие, что , то точка называется точкой разрыва первого рода.

Точка разрыва второго рода. Если хотя б один из пределов или не существует или равен бесконечности, то точка называется точкой разрыва второго рода.

Точка устранимого разрыва. Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции в точке : 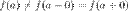или функция не определена в точке , то точка называется точкой устранимого разрыва.

Теорема1. Пусть заданы две функции и 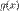, непрерывные на некотором множестве . Сумма, произведение и частное (при условии, что ) является также непрерывной функцией на рассматриваемом множестве.

Пусть функция задана на множестве , а - множество значений этой функции. Пусть на множестве задана функция , которая называется композицией функций (или сложной функцией) .

Теорема2. Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда композиция этих функций непрерывна в точке .

Теорема3. Если функция является непрерывной и строго монотонной на отрезке , которые лежит на оси абсцисс, то и обратная функция также непрерывна и монотонна на некотором отрезке оси ординат.