
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предел функции, основные теоремы о пределах. Два замечательных предела. Бесконечно малые и бесконечно большие функции.
|
|
Постоянное число а называется пределом последовательности {xn}, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения xn , у которых n> N, удовлетворяют неравенству |xn-a|< ε. (6.1)
Записывают это следующим образом:  или xn→ a.
или xn→ a.
Неравенство (6.1) равносильно двойному неравенству a-ε < xn< a+ε, (6.2)
которое означает, что точки xn, начиная с некоторого номера n> N, лежат внутри интервала (a-ε, a+ε), т.е. попадают в какую угодно малую ε -окрестность точки а.
Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции xn=f(n) целочисленного аргумента n.
Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.
Это определение называют определением предел функции по Гейне.
Определение 2. Постоянное число А называется предел функции f(x) при x→ a, если, задав произвольное как угодно малое положительное число ε, можно найти такое δ > 0 (зависящее от ε), что для всех x, лежащих в ε -окрестности числа а, т.е. для x, удовлетворяющих неравенству 0< x-a< ε, значения функции f(x) будут лежать в ε -окрестности числа А, т.е. |f(x)-A|< ε. Это определение называют определением предел функции по Коши, или “на языке ε - δ “.
Определения 1 и 2 равносильны. Если функция f(x) при x→ a имеет предел, равный А, это записывается в виде  (6.3)
(6.3)
В том случае, если последовательность {f(xn)} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), предел которой равен нулю, называется бесконечно малой величиной. Переменная величина, предел которой равен бесконечности, называется бесконечно большой величиной.
Чтобы найти предел на практике пользуются следующими теоремами.
Теорема 1. Если существует каждый предел 
 (6.4)
(6.4) 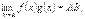 (6.5)
(6.5)  (6.6)
(6.6)
Замечание. Выражения вида 0/0, ∞ /∞, ∞ -∞, 0*∞, - являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и найти предел такого вида носит название “раскрытие неопределенностей”.
Теорема2 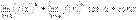 . (6.7)
. (6.7)
т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,  ;
;
 (6.8)
(6.8)  (6.9)
(6.9)
Теорема 3. 
 (6.10)
(6.10)  (6.11)
(6.11)
где e → 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первого замечательного предела и второго замечательного предела.
Используются на практике и следствия формулы (6.11):
 (6.12)
(6.12)  (6.13)
(6.13)  (6.14)
(6.14)
в частности предел, 
Функция  называется бесконечно малой функцией (б.м.ф.) при
называется бесконечно малой функцией (б.м.ф.) при  (или в точке
(или в точке  ), если
), если 