
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифференциал функции, его аналитический и геометрический смысл. Применение дифференциала для приближенных вычислений.
|
|
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
 Дифференциал функции y=f (x) равен произведению её производной на приращение независимой переменной x (аргумента).
Дифференциал функции y=f (x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:  или
или  или
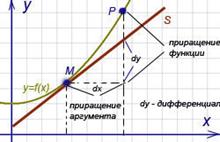
или  Геометрический смысл дифференциала. Дифференциал функции y=f (x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину
Геометрический смысл дифференциала. Дифференциал функции y=f (x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину  .
.
Приращение  функции
функции  представимо в виде:
представимо в виде:  где функция
где функция 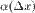 является б.м. функцией при стремлении аргумента
является б.м. функцией при стремлении аргумента  к нулю. Так как
к нулю. Так как  , то
, то  . В силу того, что второе слагаемое
. В силу того, что второе слагаемое  является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому 
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула: 