Производная сложной функции. Логарифмическое дифференцирование. Производная неявной функции. Дифференцирование параметрической функции.

Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру, смотрится очень внушительно, но сложной эта функция не является, в отличие от .

Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f –функция арктангенса, а g(x)=lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f –функция возведения в четвертую степень, а - целая рациональная функция, тогда В свою очередь, g(x) также может быть сложной функцией. Например, . Условно такое выражение можно обозначить как . Здесь f – функция синуса, - функция извлечения квадратного корня, - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом .

Формула нахождения производной сложной функции.

Логарифмическое дифференцирование. Для функций вида для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.

Вначале находится логарифм заданной функции, а уже затем вычисляется от него производная.

Пусть задана некоторая функция . Прологарифмируем левую и правую части данного выражения:

Далее продифференцируем полученное равенство при условии, что 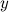является функцией от , то есть найдем производную сложной функции:

А тогда, выражая искомую производную 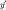, в результате имеем:

Если независимая переменная и функция 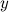связаны уравнением вида , которое не разрешено относительно 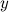, то функция 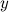называется неявной функцией переменной .

Всякую явно заданную функцию 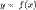можно записать в неявном виде . Обратно сделать не всегда возможно.

Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию y как функцию от x, а затем из полученного уравнения найти производную .

Предположим, что функциональная зависимость от не задана непосредственно , а через промежуточную величину — t. Тогда формулы задают параметрическое представление функции одной переменной.

Пусть функция задана в параметрической форме, то есть в виде: где функции и определены и непрерывны на некотором интервале изменения параметра . Найдем дифференциалы от правых и левых частей каждого из равенств:

Далее, разделив второе уравнение на первое, и с учетом того, что , получим выражение для первой производной функции, заданной параметрически:

Для нахождения второй производной выполним следующие преобразования: