Разложение функции в степенные ряды. Ряды Тейлора и Маклорена.

Если функция 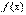в некотором интервале раскладывается в степенной ряд по степеням 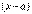, то это разложение единственно и задается формулой:

- формула Тейлора.

Частный случай формулы Тейлора, когда :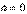
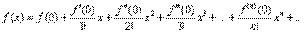- формула Маклорена

49. Периодические функции. Периодические процессы. Гармонический анализ. Функция y=F(x) с областью определения D называется периодической, если существует хотя бы одно число T> 0, такое, при котором выполняются следующие два условия:

1) точки x+T, x-T принадлежат области определения D для любого ;

2) для каждого x из D имеет место соотношение f(x)=f(x+T)=F(x-T)

Периодической функцией является такая функция, значения которой повторяются через некоторый промежуток. Например, функция y=sin x - периодическая с периодом.

50. Тригонометрический ряд Фурье. Разложение в ряд Фурье четных и нечетных функций.

Пусть функция f(x) периодична с периодом T, то есть для любого x выполнено соотношение f(x+T) = f(x).Тригонометрическим рядом Фурье функции f(x) называется функциональный ряд вида:
. Числа называются коэффициентами Фурье функции f(x). Все входящие в ряд Фурье функции также периодичны с периодом T.

Чётные функции.

Пусть f(x) –чётная, тогда b_n=0 (n=1, 2, …) => чётная функция разлагается в ряд Фурье по косинусам:

f(x) =,

где =,, (n=1, 2, 3…)

Аналогично нечётная функция по синусам:

f(x) =,

где, (n=1, 2, 3…)

51.Общие сведения о дифференциальных уравнениях. Решение дифференциальных уравнений первого порядка: с разделяющимися переменными, однородных.

Дифференциальное уравнение 1-го порядка – ур-ие F(x, y, y′) (1), связывающее между собой независим. переменную, неизвестную функцию и её производную

Если уравнение можно записать в виде y′ =f(x, y), то оно разрешимо относительно производной. Записывают так: dy = f(x, y) dx или P(x, y) dx+Q(x, y) dy=0 (дифференциальная форма)

Решение (или интеграл) диф. Ур-ия 1-го порядка – любая функция y=φ (x), которая при подстановке в ур-ие обращает его в тождество. График – интегральная кривая.

Процесс – интегрирование.

Задача отыскания решения дифференциального уравнение 1-го порядка, удовл. Заданному начальному условия y(x₀), называется задачей Коши.

=> Общее решение уравнения – функция y=φ (x, C) (2), где С - произвольная постоянная, что:

1) При любом значении С она является решением этого уравнения;

2) для любого допустимого начального условия y(x_о)=y_о найдётся такое найдётся такое значение постоянной С=С_о, что φ (x_о, C_о)=y_о

Иногда общее решение ур-ия необходимо записывать в неявном виде: φ (x, y, C)=0. Тогда это соотношение – общий интеграл ур-ия

Однородным дифференциальным уравнением первого порядка, называется уравнение, имеющее вид

Подстановка;;, где преобразует это уравнение к уравнению с разделяющимися переменными.

,,.

Однородные: Функция F(x, y) называется однородной степени k, если F(ƛ x, ƛ y)=ƛ F(x, y), где 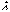- некоторая константа. Например, функция является однородной функцией степени два, поскольку .

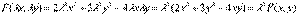А функция является однородной функцией нулевой степени однородности, так как .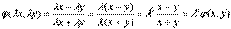

Поэтому общий вид однородного дифференциального уравнения часто записывают как 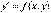, где 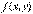- однородная функция нулевой степени однородности.