Парабола, каноническое уравнение параболы. Исследование форм параболы по ее уравнению - практика.

Парабола — геометрическое место точек, равноудалённых от даннойпрямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Каноническое уравнение параболы в прямоугольной системе координат: y2=2⋅ p⋅ x,

{\displaystyle \textstyle y^{2}=2px, p> 0 (или {\displaystyle \textstyle x^{2}=2py}, если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии {\displaystyle {\frac {p}{2}}} от обоих.

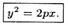1. В уравнении переменная у входит в четной степени, значит, парабола симметрична относительно оси Ох; ось Ох является осью сим­метрии параболы.

2. Так как ρ > 0, то из (11.13) следует, что х> 0. Следовательно, парабола рас­положена справа от оси Оу.

3. При имеем у = 0. Следователь­но, парабола проходит через начало коор­динат.

4. При неограниченном возрастании x модуль у также неограниченно возраста­ет.

Точ­ка О (0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М.

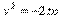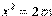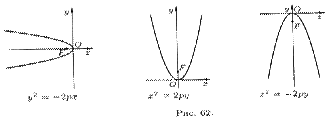
Уравнения , , 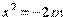(p> 0) также определяют параболы, они изображены на рисунке 62.

Нетрудно показать, что график квадратного трехчлена 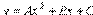, где 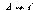, B и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.

Основные понятия, предел функции двух переменных, непрерывность функции двух переменных.

Определение. Если каждой паре (x, y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y², u=xy+z² и т.д.

Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.

Упорядоченная пара чисел (x, y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x, y).

Чтобы задать функцию z=f(x, y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.

Если каждой совокупности значений переменных x, y, z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x, y, z…t и записывается w=f(x, y, z…t).

Для функции трех переменных областью определения является упорядоченная тройка чисел (x, y, z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования.

Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x, y), заданной на некотором множествеD точек плоскости ХОУ, называется множество точек (x, y, z) пространства, у которых (x, y) принадлежит D, а z=f(x, y). В наиболее простых случаях такой график представляет собой некоторую поверхность.

Определение. Число А называется пределом функции f(M), где М(x₁, x₂, …x_n) – точка n-мерного пространства, при стремлении точки М к точке М₀(x₁⁰, x₂⁰, …x_n⁰) любым образом, если для всякого сколь угодно малого 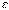> 0 существует такое число 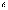> 0, что из условия 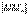< 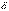, где 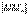- расстояние между точками М и М₀, следует < .

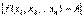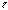Обозначается:

А.

Пусть z=f(x, y). Придадим x и y приращения 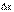и 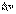. Получим приращение 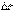функции z=f(x, y). Если 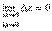, т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.

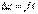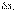Распишем x₀+ y+ 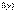-f(x₀, y₀) и положим x₀₊ x=x, y₀+ , то выражение(1) можно записать в виде 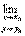f(x, y)=f(x ₀, y₀), т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.