Степенные ряды. Радиус сходимости. Дифференцирование и интегрирование степенных рядов.

Выражение вида: 1.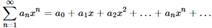

Где а₀, а₁, а₂, …, а_n, … - постоянные числа (действительные или комплексные), а х – переменная величина (действит. или комплекс.) называется степенным рядом. Числа а₀, а₁, а₂, …, а_n, … - коэффициенты степенного ряда.

Часто рассматривается также ряд, расположенный по степеням (x− x₀), то есть ряд более общего вида: 2.

(где − действительное число), частным случаем которого при = 0 являются обычные степенные ряды. (1)

Область сходимости – множество всех тех значений переменной, при которых данный степенной ряд сходится. При х=0 всякий степенной ряд вида (1 и 2) сходится, поэтому область сходимости степенного ряда содержит по крайней мере одну точку.

Теорема Абеля. Если степенной ряд сходится в точке, то он абсолютно сходится в каждой точке x, для которой |x|< ||

Следствие. Если степенной ряд расходится при некотором значении x =, то он расходится и при всех значениях x, для которых |x|> ||

Интервалом сходимости ряда (1 и 2) называется такой интервал (-R, R) (так же, (-R, +R)), что в каждой точке ряд абсолютно сходится, а в каждой точке вне отрезка [-R, R] ряд расходится. На границах сходимости (в точках x=R и так же х=х₀) ряд может как сходится, так и расходится. Число R – радиус сходимости

Всюду сходящийся ряд – если R=0, то область сходимости состоит из одной точки 0 или => область сходимости – вся числовая прямая)

Круг сходимости – открытый круг |x|< R(|x-a|< R), что в каждой его точке ряд абсолютно сход., а в каждой точке вне замкнутого круга |x|R(|x-a|R) ряд расходится.

Радиус и интервал сходимости можно вычислить, воспользовавшись радикальным признаком Коши, по формуле

или на основе признака Даламбера: