Асимптоты гиперболы.

Определение. Прямая называется асимптотой кривой, если при удалении от начала координат расстояние между ними стремится к нулю.

Уточним понятие расстояния от кривой L до прямой. Пусть М – произвольная (текущая) точка кривой L. Опустим из точки М перпендикуляр MN на прямую. Тогда наименьшее возможное значение длины этого перпендикуляра 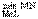называется расстоянием от кривой L до данной прямой.

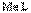Пусть дана прямая и кривая L. Пусть – точка на кривой L, 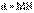– длина перпендикуляра, опущенного на прямую а из точки М, – длина отрезка прямой, проходящей через точку М параллельно оси ординат, заключенного между прямой а и кривой L. Из построения следует, что если М(х, у) – координаты точки М, то –координаты точки . По определению, прямая а является асимптотой кривой L тогда и только тогда, когда 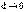при . В свою очередь .

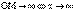Таким образом, прямая а является асимптотой кривой L тогда и только тогда, когда .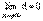

Теорема. Для того, чтобы прямая а была асимптотой для кривой L необходимо и достаточно, чтобы .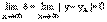

Доказательство. Угол между прямой а и осью ординат Оу остается неизменным при любом расположении точки М на кривой L и не равным нулю (мы предполагаем, что прямая 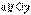). Из прямоугольного треугольника MNK следует, что 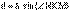, где 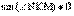. Отсюда,

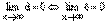. Теорема доказана.