
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
|
|
Если заданы координаты трех точек A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле
| x - x1 | y - y1 | z - z1 | = 0 |
| x2 - x1 | y2 - y1 | z2 - z1 | |
| x3 - x1 | y3 - y1 | z3 - z1 | |
 36. Каноническое уравнение прямой в пространстве.
36. Каноническое уравнение прямой в пространстве.
Получим канонические уравнения прямой a в трехмерном пространстве.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую: укажем точку, через которую проходит прямая a, и направляющий вектор прямой a. Будем считать, что точка 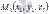 лежит на прямой а и
лежит на прямой а и  - направляющий вектор прямой а.
- направляющий вектор прямой а.
Очевидно, что множество точек  трехмерного пространства определяет прямую а тогда и только тогда, когда векторы
трехмерного пространства определяет прямую а тогда и только тогда, когда векторы  и
и  коллинеарны.
коллинеарны.
Запишем необходимое и достаточное условие коллинеарности векторов  и
и  в координатной форме. Для этого нам нужно знать координаты этих векторов. Координаты вектора
в координатной форме. Для этого нам нужно знать координаты этих векторов. Координаты вектора 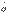 нам известны из условия. Осталось вычислить координаты вектора
нам известны из условия. Осталось вычислить координаты вектора  - они равны разности соответствующих координат точек
- они равны разности соответствующих координат точек  и
и  , то есть,
, то есть,  (при необходимости смотритенахождение координат вектора по координатам точек). Теперь записываем условие коллинеарности векторов
(при необходимости смотритенахождение координат вектора по координатам точек). Теперь записываем условие коллинеарности векторов  и
и  :
:
 , где
, где  - произвольное действительное число (при
- произвольное действительное число (при  точки
точки  и
и  совпадают, что нас тоже устраивает).
совпадают, что нас тоже устраивает).
Если 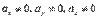 , то каждое уравнение системы
, то каждое уравнение системы  можно разрешить относительно параметра
можно разрешить относительно параметра  и приравнять правые части:
и приравнять правые части:

Полученные уравнения вида  в заданной прямоугольной системе координат Oxyz определяют прямую a. Уравнения
в заданной прямоугольной системе координат Oxyz определяют прямую a. Уравнения  есть канонические уравнения прямой в трехмерном пространстве в прямоугольной системе координат Oxyz. Их также называют уравнениями прямой в пространстве в каноническом виде.
есть канонические уравнения прямой в трехмерном пространстве в прямоугольной системе координат Oxyz. Их также называют уравнениями прямой в пространстве в каноническом виде.