
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Касательная плоскость и нормаль к поверхности
|
|
Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точкуМ0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x, y), в точке M0(x0, y0, z0) имеет вид:
z – z0 = f’x(x0, y0)(x – x0) + f’y(x0, y0)(y – y0)
Вектор  называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости. Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N. Канонические уравнения нормали к поверхности, заданной уравнением z = f(x, y), в точке M0(x0, y0, z0), где z0 = f(x0, y0), имеют вид:
называется вектором нормали к поверхности σ в точке М0. Вектор нормали перпендикулярен касательной плоскости. Нормалью к поверхности σ в точке М0 называется прямая, проходящая через эту точку и имеющая направление вектора N. Канонические уравнения нормали к поверхности, заданной уравнением z = f(x, y), в точке M0(x0, y0, z0), где z0 = f(x0, y0), имеют вид: 
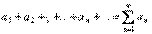 45.Знакопостоянные числовые ряды. Необходимый признак сходимости числового ряда. Признаки сравнения. Признаки сходимости: Даламбера, радикальный признак Коши, интегральный признак Коши.
45.Знакопостоянные числовые ряды. Необходимый признак сходимости числового ряда. Признаки сравнения. Признаки сходимости: Даламбера, радикальный признак Коши, интегральный признак Коши.
1. Основные определения.
Пусть дна числовая последовательность a1, a2, …, an, … Выражение вида (1)
называется числовым рядом.
Числа a1, a2, …, an … называются членами ряда, а член an с произвольным номером - общим членом ряда.
Суммы конечного числа членов ряда  называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм S1, S2, S3, …, Sn, … (2).
называются частичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм S1, S2, S3, …, Sn, … (2).
Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S, которое в этом случае называется суммой ряда (1). Символически это записывается так:  или
или  .
.
Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящимся.
Для сходимости ряда (1) необходимо и достаточно, чтобы для любого  существовало число
существовало число  такое, что при
такое, что при  и
и  (n и p – натуральные числа) было выполнено неравенство
(n и p – натуральные числа) было выполнено неравенство  .
.
В частности, если ряд сходится, то  .
.
Теорема 4: Если ряд 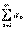 сходится, то его общий член стремиться к нулю, т.е.
сходится, то его общий член стремиться к нулю, т.е.  .
.
Доказательство. По условию ряд  сходится. Обозначим через S его сумму. Рассмотрим частные суммы ряда
сходится. Обозначим через S его сумму. Рассмотрим частные суммы ряда  и
и  . Отсюда
. Отсюда  . Т.к.
. Т.к.  и
и  при
при 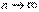 , то
, то
 .
.
Условие  является необходимым, но не достаточным условием сходимости ряда.
является необходимым, но не достаточным условием сходимости ряда.
Признак сравнения 1.
Теорема 5: Для того чтобы ряд  с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.
с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.
Доказательство. Необходимость. Пусть ряд 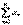 сходится. Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящая последовательность является ограниченной.
сходится. Это значит, что последовательность его частичных сумм имеет предел. Всякая сходящая последовательность является ограниченной.
Достаточность. Пусть последовательность частичных сумм ряда 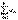 ограничена. Т.к. ряд
ограничена. Т.к. ряд 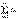 с неотрицательными членами, то его частичные суммы образуют не убывающую последовательность:
с неотрицательными членами, то его частичные суммы образуют не убывающую последовательность:  . Монотонная ограниченная последовательность сходится, т.е. сходится ряд
. Монотонная ограниченная последовательность сходится, т.е. сходится ряд  .
.
Признак сравнения 2.
Теорема 6: Пусть даны два ряда с неотрицательными членами  и
и  и для всех n выполняется неравенство
и для всех n выполняется неравенство 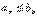 . Тогда из сходимости ряда
. Тогда из сходимости ряда  следует сходимость ряда
следует сходимость ряда  , а из сходимости ряда
, а из сходимости ряда  следует сходимость ряда
следует сходимость ряда  .
.
Доказательство. Обозначим через  и
и  соответственно частичные суммы рядов
соответственно частичные суммы рядов  и
и  . Из неравенства
. Из неравенства 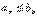 следует, что
следует, что  (7)
(7)
Если ряд  сходится, то по теореме 5 (необходимость) последовательность его частичных сумм ограничена, т.е. для любого n
сходится, то по теореме 5 (необходимость) последовательность его частичных сумм ограничена, т.е. для любого n  , где М – некоторое число. Но тогда по формуле (7) и
, где М – некоторое число. Но тогда по формуле (7) и 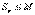 , откуда по той же теореме 5 (достаточность) следует, что ряд
, откуда по той же теореме 5 (достаточность) следует, что ряд  сходится.
сходится.
Если же ряд  расходится, то ряд
расходится, то ряд  также расходится, т.к., допустив сходимость ряда
также расходится, т.к., допустив сходимость ряда  получим по только что доказанному сходимость ряда
получим по только что доказанному сходимость ряда  , а это противоречит условию теоремы.
, а это противоречит условию теоремы.
Признак Даламбера.
Теорема 7: Пусть дан ряд  с положительными членами и существует предел
с положительными членами и существует предел 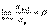 . Тогда а) при
. Тогда а) при 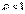 ряд сходится; b) при
ряд сходится; b) при 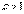 ряд расходится.
ряд расходится.
Доказательство.
a) Пусть  и
и  . Докажем, что ряд
. Докажем, что ряд  сходится. По определению предела числовой последовательности для любого
сходится. По определению предела числовой последовательности для любого  существует номер N такой, что при
существует номер N такой, что при  выполняется неравенство
выполняется неравенство  . Отсюда следует, что
. Отсюда следует, что  . (8)
. (8)
Т.к. 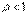 , то
, то  можно взять настолько малым, что будет выполнено неравенство
можно взять настолько малым, что будет выполнено неравенство  . Полагая
. Полагая  , на основании правого из неравенств (8) имеем
, на основании правого из неравенств (8) имеем  , или
, или  для n=N, N+1, N+2, … Придавая n эти значения, из последнего неравенства получаем
для n=N, N+1, N+2, … Придавая n эти значения, из последнего неравенства получаем
 т.е. члены ряда
т.е. члены ряда  (9) меньше соответствующих членов ряда, составленного из элементов геометрической прогрессии:
(9) меньше соответствующих членов ряда, составленного из элементов геометрической прогрессии:  (10)
(10)
Т.к.  , то ряд (10) сходится. Тогда согласно признаку сравнения ряд (9) также сходится. Но ряд (9) получен из данного ряда
, то ряд (10) сходится. Тогда согласно признаку сравнения ряд (9) также сходится. Но ряд (9) получен из данного ряда  в результате отбрасывания конечного числа первых членов, следовательно, по теореме 1 ряд
в результате отбрасывания конечного числа первых членов, следовательно, по теореме 1 ряд  сходится.
сходится.
b) Пусть теперь  . Докажем, что ряд
. Докажем, что ряд 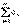 расходится. Возьмем
расходится. Возьмем  настолько малым, чтобы
настолько малым, чтобы  . Тогда при
. Тогда при  в силу левого из неравенств (8) выполняется неравенство
в силу левого из неравенств (8) выполняется неравенство 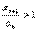 или
или 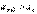 . Таким образом, члены ряда, начиная с некоторого номера N, возрастают с увеличением их номеров, т.е. общий член ряда
. Таким образом, члены ряда, начиная с некоторого номера N, возрастают с увеличением их номеров, т.е. общий член ряда  не стремится к нулю при
не стремится к нулю при 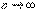 . Следовательно, согласно теореме 4, ряд
. Следовательно, согласно теореме 4, ряд  расходится.
расходится.
Замечание. При  ряд
ряд  может, как сходится, так и расходится. В этом случае необходимо дополнительное исследование ряда с помощью признака сравнения или других признаков.
может, как сходится, так и расходится. В этом случае необходимо дополнительное исследование ряда с помощью признака сравнения или других признаков.
Признак Коши.
Теорема 8: Пусть дан ряд 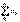 с положительными членами.
с положительными членами.
a) Если 
 (11) то он сходится; если же
(11) то он сходится; если же 
 (12), то он расходится.
(12), то он расходится.
b) Если 
 , (13) то при q< 1 ряд
, (13) то при q< 1 ряд 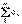 сходится, а при q> 1 расходится, и при этом
сходится, а при q> 1 расходится, и при этом 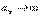 .
.
c) Если верхний предел 
 , (14) то ряд
, (14) то ряд 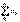 при q< 1 сходится, а при q> 1 расходится и при этом общий член
при q< 1 сходится, а при q> 1 расходится и при этом общий член  ряда не ограничен.
ряда не ограничен.
Интегральный признак Коши.
Теорема 9: Пусть дан ряд  ,
,
члены которого являются значениями некоторой функции f(x), положительной, непрерывной и убывающей на полуинтервале [1, +¥). Тогда, если  сходится, то сходится и ряд
сходится, то сходится и ряд  также расходится.
также расходится.