Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона: 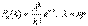– среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для и . При больших 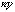рекомендуется применять формулы Лапласа. События, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала.

62.Случайные величины: основные понятия, дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины.

Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2, …, 25.

Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4).

Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.
Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.

Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:

Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х ₁, х ₂, …, х_n. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = х_i (i = 1, 2, …, n) образуют полную группу попарно независимых событий. Следовательно, р ₁ + р ₂+ … + р_n = 1.
Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения.

Законом распределения дискретной случайной величины называется соответствие между отдельными возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины проще представить в виде таблицы распределения, в первой строке которой указывают возможные значения случайной величины, а во второй строке — соответствующие вероятности этих значений.

Здесь х₁, х₂, x₃, х₄,..., х_n — значения, которые может принять случайная дискретная величина X и соответствующие вероятности

p₁=Р(Х=х₁), p₂=Р(Х=х₂),

p₃=Р(Х=х₃), p₄=Р(Х=х₄).
p_n=Р(Х = х_n) и p₁+p₂+p₃+p₄+...+p_n=1.

63. Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия, среднеквадратичное отклонение, мода.

Функция распределения содержит полную информацию о случайной величине. На практике функцию распределения не всегда можно установить; иногда такого исчерпывающего знания и не требуется. Частичную информацию о случайной величине дают числовые характеристики, которые в зависимости от рода информации делятся на следующие группы.

1.Характеристики положения случайной величины на числовой оси (мода Мo, медиана Мe, математическое ожидание М(Х)).

2.Характеристики разброса случайной величины около среднего значения (дисперсия D(X), среднее квадратическое отклонение σ (х)).

3.Характеристики формы кривой y = φ (x) (асимметрия As, эксцесс Ех).

Рассмотрим подробнее каждую из указанных характеристик.

Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений: 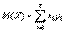. (2.4)

Для непрерывной случайной величины Х, имеющей заданную плотность распределения φ (x) математическим ожиданием называется следующий интеграл:

. (2.5)

Здесь предполагается, что несобственный интеграл

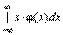сходится абсолютно, т.е. существует.

Свойства математического ожидания:

1. М(С) = C, где С = const;

2. M(C ∙ Х) = С ∙ М(Х);

3. М(Х ± Y) = М(Х) ± М(Y), где X и Y – любые случайные величины;

4. М(Х ∙ Y)= М(Х)∙ М(Y), где X и Y – независимые случайные величины.

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис. 2.3), а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис. 2.4).

Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е. Р(Х < Ме) = Р(X > Ме)

Из определения медианы следует, что Р(Х < Ме) = 0, 5, т.е. F (Ме) = 0, 5. Геометрически медиану можно истолковывать как абсциссу, в которой ордината φ (x) делит пополам площадь, ограниченную кривой распределения (рис. 2.5). В случае симметричного распределения медиана совпадает с модой и математическим ожиданием.

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания D(X) = M(X – М(Х))².

Дисперсию случайной величины Х удобно вычислять по формуле:

а) для дискретной величины ; (2.6)

б) для непрерывной случайной величины 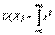j(х)d x – [M(X)]² . (2.7)

Дисперсия обладает следующими свойствами:

1. D(C) = 0, где С = const;

2. D(C × X) = C²∙ D(X);

3. D (X ± Y) = D (X) + D (Y), если X и Y независимые случайные величины.

Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е. σ (X) = .

Заметим, что размерность σ (х) совпадает с размерностью самой случайной величины Х, поэтому среднее квадратическое отклонение более удобно для характеристики рассеяния.

Обобщением основных числовых характеристик случайных величин является понятие моментов случайной величины.

Функция распределения вероятностей непрерывной случайной величины (определение, свойства, график), плотность распределения вероятностей непрерывной случайной величины (определение, свойства, график).

Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.

Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е. F(x) = P (X < x).

Иногда функцию F(x) называют интегральной функцией распределения.

Функция распределения обладает следующими свойствами:

1.Значение функции распределения принадлежит отрезку [0, 1]: 0 ≤ F(x) ≤ 1.

2.Функции распределения есть неубывающая функция.

3.Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале: Р(а < X < b) = F(b) – F(а). (2.1)

4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то

F(x) = 0 при х ≤ а;   F(x) = 1 при х ≥ b.

4.Справедливы следующие предельные отношения: .

5.Для дискретной случайной величины Х, которая может принимать значения х ₁, х ₂, …, х_n, функция распределения имеет вид где неравенство под знаком суммы означает, что суммирование касается всех тех значений х_i, величина которых меньше х.

Поясним эту формулу исходя из определения функции F(x). Предположим, что аргумент х принял какое-то определенное, но такое, что выполняется неравенство x_i < x ≤ x_{i +1}. Тогда левее числа х на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1, 2, 3, …, i. Поэтому неравенство Х < x выполняется, если величина Х примет значения х_к, где k = 1, 2, …, i. Таким образом, событие Х < x наступит, если наступит любое, неважно какое, из событий Х = х ₁, Х = х ₂, Х = х ₃, …, Х = х_i. Так как эти события несовместны, то по теореме сложения вероятностей имеем Предположим теперь, что для непрерывной случайной величины Х ее функция распределения F(x) имеет непрерывную производную F'(x)= φ (x).

Функцию φ (x) называют плотностью вероятности (для данного распределения) или дифференциальной функцией.

Так как плотность вероятности φ (x) является производной неубывающей функции F(x), то она неотрицательна: φ (x)≥ 0. В отличие от функции распределения, плотность вероятности может принимать сколь угодно большие значения.

Так как F(x) является первообразной для φ (x), то на основании формулы Ньютона-Лейбница имеем . Отсюда в силу (3.1) получаем P(a ≤ X ≤ b) = .

Полагая а =–∞ и b =+∞, получаем достоверное событие Х принадлежащее (–∞, +∞), вероятность которого равна единице. Следовательно, . В частности, если все возможные значения случайной величины при­надлежат интервалу (а, b), то . Полагая в формуле а = –∞, b = х и обозначая для ясности переменную интегрирования t, получим функцию распределения F(x) = P (– ∞ < X < x) = .

65.Нормальное распределение. Кривая Гаусса. Влияние параметров µ и σ на форму кривой Гаусса. Вероятность попадания нормально распределенной случайной величины в заданный интервал Правило «трех сигм».

Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории вероятностей и занимает среди других законов распределения особое положение. Это – наиболее часто встречающийся на практике закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, ошибки стрельбы и т.д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах её закон распределения.

Теоремы, устанавливающие нормальный закон как предельный для суммы независимых равномерно малых случайных слагаемых, будут подробнее рассмотрены в главе 13.

Нормальный закон распределения характеризуется плотностью вероятности вида:

(6.1.1)

Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 6.1.1). Максимальная ордината кривой, равная , соответствует точке ; по мере удаления от точки плотность распределения падает, и при кривая асимптотически приближается к оси абсцисс.

Выясним смысл численных параметров и , входящих в выражение нормального закона; докажем, что величина есть не что иное, как математическое ожидание, а величина - среднее квадратическое отклонение величины . Для этого вычислим основные числовые характеристики величины - математическое ожидание и дисперсию.

Применяя замену переменной

имеем: (6.1.2)

Нетрудно убедиться, что первый из двух интервалов в формуле (6.1.2) равен нулю; второй представляет собой известный интеграл Эйлера-Пуассона: 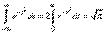. (6.1.3)

Следовательно, , т.е. параметр представляет собой математическое ожидание величины . Этот параметр, особенно в задачах стрельбы, часто называют центром рассеивания (сокращенно – ц. р.).

Вычислим дисперсию величины : .

Применив снова замену переменной

имеем: .

Интегрируя по частям, получим .

Первое слагаемое в фигурных скобках равно нулю (так как при убывает быстрее, чем возрастает любая степень ), второе слагаемое по формуле (6.1.3) равно , откуда .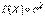

Следовательно, параметр в формуле (6.1.1) есть не что иное, как среднее квадратическое отклонение величины .

Выясним смысл параметров 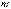и нормального распределения. Непосредственно из формулы (6.1.1) видно, что центром симметрии распределения является центр рассеивания . Это ясно из того, что при изменении знака разности на обратный выражение (6.1.1) не меняется. Если изменять центр рассеивания , кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 6.1.2). Центр рассеивания характеризует положение распределения на оси абсцисс.

Размерность центра рассеивания – та же, что размерность случайной величины .

Параметр характеризует не положение, а самую форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна ; при увеличении максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 6.1.3 показаны три нормальные кривые (I, II, III) при ; из них кривая I соответствует самому большому, а кривая III – самому малому значению . Изменение параметра равносильно изменению масштаба кривой распределения – увеличению масштаба по одной оси и такому же уменьшению по другой.

Размерность параметра , естественно, совпадает с размерностью случайной величины .

В некоторых курсах теории вероятностей в качестве характеристики рассеивания для нормального закона вместо среднего квадратического отклонения применяется так называемая мера точности. Мерой точности называется величина, обратно пропорциональная среднему квадратическому отклонению : .

Размерность меры точности обратная размерности случайной величины. Термин «мера точности» заимствован из теории ошибок измерений: чем точнее измерение, тем больше мера точности. Пользуясь мерой точности , можно записать нормальный закон в виде: .