Бесконечно малые и бесконечно большие последовательности, связь между ними,(с доказательством)

Определение 1: Последовательность (х_n) называется бесконечно малой, если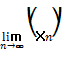

Или другими словами: последовательность (х_n) называется бесконечно малой, если для любого числа ε > 0 можно найти такой номер N, что для всех n> N выполняется неравенство |x_n|< ε

Пример:

Последовательность (1/n) бесконечно малая, так как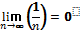

Определение 2: Последовательность (х_n) называется бесконечно большой, если для любого числа ε > 0, можно найти такой номер N, что для всех n> N, выполняется неравенство |x_n|> ε.

Если последовательность бесконечно большая, то или х_n^----→ _{n→ ∞} ∞

Пример:

((-1)ⁿ∙ n)

-1, 2, -3 … эта последовательность бесконечно большая

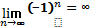
Установим связь между бесконечно малой последовательностью и бесконечно большой последовательностью

Теорема: 1)Если последовательность (х_n)- бесконечно малая, то последовательность (1/x_n) – бесконечно большая.

2) Если последовательность (х_n) бесконечно большая, то последовательность (1/x_n) – бесконечно малая.

Докажем первую часть теоремы:

Дано: (х_n)- бесконечно малая последовательность

Доказать: (1/x_n) – бесконечно большая последовательность

Доказательство: Берем любое число E> 0 и запишем число ε =1/Е> 0. По данному (х_n)- бесконечно малая последовательность, то есть для любого числа ε > 0, можно найти такой номер N, что n> N, выполняется неравенство |x_n|< ε или |x_n|< 1/E или 1/|x_n|> E что и требовалось доказать.

24. Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.

Из этого определения вытекает, что если ранг матрицы равен r, то

среди миноров этой матрицы есть по крайней мере один минор r-го

порядка, отличный от нуля (его будем называть базисным минором),

а все миноры порядка 1 + r и выше равны нулю. Ранг матрицы А обозначается r (А). По определению, ранг нулевой матрицы О равен нулю; тогда ранг r (А) произвольной матрицы А_m’n удовлетворяет неравенству 0≤ r (А) ≤ min(n, m)

Поскольку вычислять ранг матрицы по определению достаточно трудоемко, то с помощью элементарных преобразований матрицу приводят к такому виду, из которого ранг матрицы очевиден.

Элементарными преобразованиями матрицы называются:

1. Транспонирование.

2. Перемена местами двух строк или двух столбцов.

3. Умножение всех элементов строки или столбца на число с, отличное от нуля.

4. Прибавление ко всем элементам строки или столбца соответствующих элементов другой строки или столбца, умноженных на одно и то же число.

Теорема 3.5. Элементарные

преобразования не меняют ранг матрицы.

Отметим, что с помощью элементарных преобразований любую матрицу А можно привести к виду

(3.9)

где на главной диагонали стоят r единиц, а все остальные элементы матрицы равны нулю. Ясно, что ранг такой матрицы равен r, тогда по

теореме 3.5. ранг матрицы А равен r.

Замечание. При вычислении ранга матрицы с помощью элементарных преобразований не обязательно получать вид (3.9), достаточно

привести матрицу к трапециевидной форме, количество ненулевых строк в которой равно рангу матрицы.