
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие производной функции в точке. Односторонние и бесконечные производные.
|
|
Пусть функция f (x) = y определена в некоторой окрестности точки x0.
Определение 8.1. Производной функции f в точке x0 называется число, обозначаемое 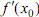 , равное пределу отношения приращения функции
, равное пределу отношения приращения функции 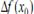 в этой точке к приращению аргумента ∆ x при стремлении ∆ x к нулю, если этот предел существует:
в этой точке к приращению аргумента ∆ x при стремлении ∆ x к нулю, если этот предел существует:
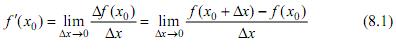
или, если обозначить 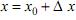 , то при
, то при 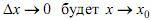 и
и
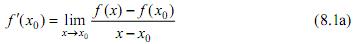
Определение 8.2. Функция, имеющая конечную производную в точке х0, называется дифференцируемой в этой точке.
Определение 8.3. Если в точкех0 функция f (x) непрерывна, а предел (8.1) равен бесконечности (+∞ или − ∞), то говорят о бесконечной производной.
Определение 8.4. Пределы
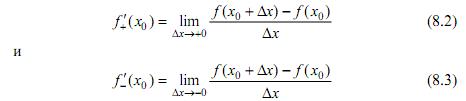
называются правосторонней и левосторонней производной, соответственно.
Для существования производной 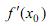 необходимо и достаточно, чтобы существовали обе односторонние производные
необходимо и достаточно, чтобы существовали обе односторонние производные 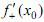 и
и 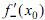 и они были равны друг другу:
и они были равны друг другу: 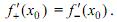
Производная обозначается и другими способами, например:
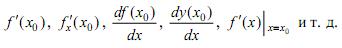
Геометрический смысл производной. Уравнения касательной и нормали к плоской кривой. Угол между кривыми.
На кривой f (x) y выберем две различные точки М0 и М1 (рис.8.1) и через них проведем единственную прямую l, которая называется секущей к графику. Используя уравнения прямой, проходящей через две заданные точки 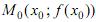 и
и 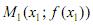 которое имеет вид
которое имеет вид 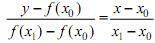 , получим уравнение секущей
, получим уравнение секущей
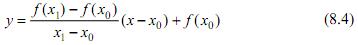
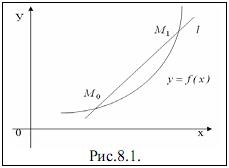
Сравнивая уравнение (8.4) с уравнением прямой с угловым ко-эффициентом, заключаем, что угловой коэффициент k секущей l имеет вид 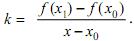
Тогда 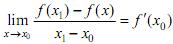 и уравнение секущей (8.4) перейдет в уравнение касательной:
и уравнение секущей (8.4) перейдет в уравнение касательной:
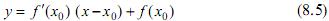
Таким образом, производная функции f (x) = y, вычисленная в точке х= х0 есть угловой коэффициент касательной, проведенной к графику функции f (x) =y в точке 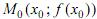
В этом и состоит геометрический смысл производной.
Определение 8.6. Прямая, перпендикулярная к касательной в точке М0 называется нормалью к кривой f (x) =y в точке М0.
Из условия k1 k2 =− 1 перпендикулярности прямых заключаем, что угловой коэффициент kн нормали выражается через угловой коэффициент kкас касательной по формуле 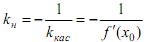 Следовательно, уравнение нормали к кривой f (x) =y в точке М0 имеет вид
Следовательно, уравнение нормали к кривой f (x) =y в точке М0 имеет вид 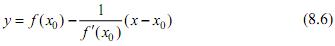
Определение 8.7. Пусть две кривые f (x) =y и g (x) = y пересекаются в точке 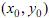 т.е.
т.е. 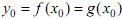 Углом α между заданными кривыми называется угол между касательными к кривым, проведенным в точке их пересечения:
Углом α между заданными кривыми называется угол между касательными к кривым, проведенным в точке их пересечения:
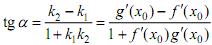
| 1. Y=c, c-const Y/=0 2. Y=x Y/=1 3. Y=u+v-w Y/=u/+v/+w/ 4. Y=u*v Y/=u/*v+u*v/ 5. Y=uvw Y/=u /vw+uv /w+uvw/ 6. Y= u/v Y/= u /v-uv/ v2 7. Y=c/v, y=cv -1 Y/= c V2 8. Y=logax, a> 0, Y/= 1 logae x 9. Y=lnx Y/= 1 | 10. Y=ax, a> 0 Y/=axlna Y=ex Y/= ex 11. Y=xL, где L- любое Y/=LxL-1 12. Y=sinx Y/=cosx 13. Y=cosx Y/=- sinx 14. Y=tgx Y/= 1__ Cos2x 15. Y=ctgx Y/= 1__ Sin2x 16. Y=arcsinx Y/= 1__ √ 1-x2 |
Док-во: x=siny
Y/= 1_ = 1____ = 1________
x/y cosy cos(arcsinx)
= 1___________ = 1___
√ 1-sin2*arccosx √ 1-x2
38. Производная обратной функции. (с доказательством)
Пусть функция y=f(x) (1), задана на множестве х (большая), а у – множество её возможных значений тогда каждому х€ Х ставится в соответствие единственное значение у€У с другой стороны каждому у€У будет соответствовать одно или несколько значений х€ Х. В случае, когда каждому у€У соответствует только одно значение х€ Х, для которого f(x)=у на множестве У можно определить функцию х=g(y) (2) множеством значений которого является множество х. Функцию (2) называют обратной по отношению к 1-ой. Функции (1) и (2) – взаимообратные функции.
Обозначают обратную функцию х= 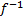 (y).
(y).
T.1: Если функция y=f(x) определена строго монотонно и непрерывна на отрезке [a, b], то обратная функция х= 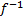 (y) определена строго монотонно и непрерывно на отрезке [А, В], где А= f(а), В= f(b). Строгая монотонность: для любых точек
(y) определена строго монотонно и непрерывно на отрезке [А, В], где А= f(а), В= f(b). Строгая монотонность: для любых точек 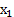 ,
, 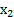 € х
€ х 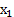 <
< 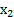 (
(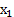 >
> 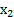 ) выполняется неравенство f(
) выполняется неравенство f(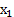 )< f(,
)< f(, 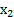 ) (f(
) (f(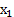 )> f(,
)> f(, 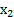 ))
))
Т.2: Пусть функция у= f(x) удовлетворяет условиям теоремы о существовании обратной функции и в точке 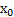 имеет конечную производную f’(
имеет конечную производную f’(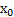 )≠ 0, тогда функция х=g(y) точке
)≠ 0, тогда функция х=g(y) точке 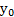 так же имеет конечную производную равную
так же имеет конечную производную равную 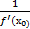 .
.
Доказательство: Придадим 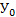 приращение
приращение 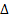 у≠ 0, тогда функция х=g(y) получит приращение
у≠ 0, тогда функция х=g(y) получит приращение 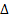 х≠ 0. Очевидно, что
х≠ 0. Очевидно, что 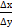 =
= 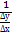 .
.
Если 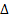 у–›0, то
у–›0, то 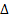 х так же –›0, что следует из непрерывности обратной функции.
х так же –›0, что следует из непрерывности обратной функции.
Переходим к пределу
Предел: lim (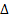 у–›0)
у–›0) 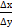 =: lim (
=: lim (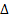 x–›0)
x–›0) 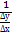 =
= 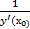 , т.е. х’y =
, т.е. х’y = 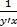 или у’х =
или у’х = 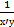 .
.
Что и требовалось доказать.
8.Эллипс(!!!! Это не надо!!!!)
Определение. Эллипсом называется кривая, заданная уравнением 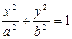 .
.
Определение. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.
Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом. е = с/a. Т.к. с < a, то е < 1.
С эллипсом связаны две прямые, называемые директрисами. Их уравнения: x = a/e; x = -a/e.