
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства бесконечно малых последовательностей (доказательство)
|
|
Теорема 1: сумма двух бесконечно малых последовательностей есть последовательность бесконечно малая.
Доказательство: (  ) (альфа) (
) (альфа) (  ) – б.м.
) – б.м.
Доказать, что (  +
+  ) – б.м., т.е. по определению для любого числа E> 0, существует N
) – б.м., т.е. по определению для любого числа E> 0, существует N
Выполн. нер-во l  +
+  l< E
l< E
Берём произвольное число Е> 0. Последовательность ( ) бесконечно малая, т.е. для любого
) бесконечно малая, т.е. для любого  > 0 существует такое число N с индексом 1, что для любых n> N выполняется l
> 0 существует такое число N с индексом 1, что для любых n> N выполняется l  l<
l<  (1),
(1),
т.к. ( ) –б.м., то для любого числа
) –б.м., то для любого числа  > 0 существует такое число N с индексом 2, что для любых n>
> 0 существует такое число N с индексом 2, что для любых n>  выполняется l
выполняется l  l <
l <  (2).
(2).
Обозначим через N = max {  :
:  }, тогда для любых n> N неравенство (1) и (2) выполняются одновременно.
}, тогда для любых n> N неравенство (1) и (2) выполняются одновременно.
Воспользуемся свойством | x+y| < = (меньше либо равно) |x| +|y|, тогда |  +
+  |< = (меньше либо равно))|
|< = (меньше либо равно))|  | +|
| +|  | <
| <  +
+ 
Таким образом неравенство |  +
+  | < E, которое выполняется для всех n> N, это значит (
| < E, которое выполняется для всех n> N, это значит (  +
+  ) – б.м.
) – б.м.
Определение: последовательность (  называется ограниченной если существует такое число М, что для любых n выполняется неравенство |
называется ограниченной если существует такое число М, что для любых n выполняется неравенство |  < = (меньше либо равно) M.
< = (меньше либо равно) M.
Теорема 2: произведение б.м. на ограниченную есть последовательность бесконечно малых.
Следствие 1: произведение б.м. на постоянное число есть последовательность б.м.
Следствие 2: произведение двух б.м. последовательностей есть последовательность б.м.
(  *
*  )- б.м.
)- б.м.
Следствие справедливо, т.к. б.м. последовательность есть последовательность ограничеснная.
Вопрос
Замечательные пределы
Определение -Предел отношения
 .
.  называется первым замечательным пределом.
называется первым замечательным пределом.
Разновидности первого замечательного предела:
1) 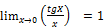
2) 
3) 
Определение- Вторым замечательным пределом
называется следующий предел 
е=2.71828182845)))) е-основание натурального алгоритма
Разновидности второго замечательного предела:
1) 
2) 
Вопрос