
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Признаки Даламбера и Коши сходимости рядов с неотрицательными членами
|
|
Признак Даламбера:
Пусть дан знакоположительный числовой ряд
 (7)
(7)
и пусть существует предел  При p< 1 ряд (7) сходится, при p> 1 ряд (7) расходится.
При p< 1 ряд (7) сходится, при p> 1 ряд (7) расходится.
Доказательство:
По условию существует предел  . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³ N выполняется условие
. Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³ N выполняется условие
 или p-E<
или p-E< 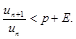 (10)
(10)
Пусть сначала p< 1. Выберем Е так, что p+E=q< 1. Для всех n³ N имеем 

 … или
… или

или
 (11)
(11)
Рассмотрим ряды:
 (12)
(12)
 . (13)
. (13)
Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.
Пусть теперь p> 1. Выберем Е так, что p-E> 1. Тогда из левой части неравенства (10) следует, что при n³ N выполняется  или un+1> un, то есть члены ряда возрастают с возрастанием номера n. Поэтому
или un+1> un, то есть члены ряда возрастают с возрастанием номера n. Поэтому  un¹ 0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
un¹ 0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.
Замечания:
1. Если расходимость ряда установлена с помощью признака Даламбера, то  un¹ 0.
un¹ 0.
2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.
3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.
Признак Коши:
Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)
и пусть существует предел 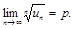 При p< 1 ряд (7) сходится, при p> 1 ряд (7) расходится.
При p< 1 ряд (7) сходится, при p> 1 ряд (7) расходится.
Доказательство:
По условию существует 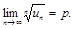 Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³ N выполняется условие |
Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³ N выполняется условие |  | < E или
| < E или
p-E<  < p+E. (14)
< p+E. (14)
Пусть p< 1. Выберем Е таким, чтобы выполнялось p+E=q< 1. Тогда из (14) получаем  < q или un< qn для всех n³ N. Рассмотрим ряды
< q или un< qn для всех n³ N. Рассмотрим ряды
 (15)
(15)
 (16)
(16)
Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un< qn для всех n³ N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).
Пусть теперь p> 1. Выберем Е так, чтобы выполнялось условие
p-E > 1. Тогда из (14) получаем  > 1 или un> 1, следовательно,
> 1 или un> 1, следовательно,  un¹ 0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.
un¹ 0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.