Уравнение с разделяющимися переменными

Дифференциальное уравнение

(3.1)

называется уравнением с разделяющимися переменными.

Умножая обе части уравнения на 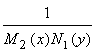, получаем уравнение

(3.2)

В уравнении (3.2) коэффициент при dx зависит только от x, а коэффициент при dy зависит только от y. Значит, в уравнении (3.2) переменные разделены. Интегрируя, получаем:

+

Линейные уравнения

В математике линейное дифференциальное уравнение имеет вид

где дифференциальный оператор L линеен, y — неизвестная функция , а правая часть — функция от той же переменной, что и y.

Линейный оператор L можно рассматривать в форме

Уравнения с переменными коэффициентами

Линейное дифференциальное уравнение порядка n с переменными коэффициентами имеет общий вид

Пример

Уравнение Коши — Эйлера, используемое в инженерии, является простым примером линейного дифференциального уравнения с переменными коэффициентами