Уравнение первого порядка

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

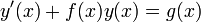
Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель

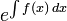
получим

используем правило дифференцирования произведения

что, после интегрирования обеих частей, дает нам

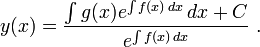
Таким образом, решение линейного дифференциального уравнения первого порядка

(в частности, с постоянными коэффициентами) имеет вид

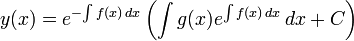
где является константой интегрирования.

Пример

Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:

Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер^{[ неизвестный термин ]} системы.

В этом случае, p (x) = b, r (x) = 1.

Следовательно, решение будет: