Случай прямоугольника

Теорема 6. Пусть для функции f (x, y) в прямоугольнике R = [ a ≤ x ≤ b ] × [ c ≤ y ≤ d ] существует двойной интеграл .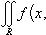

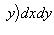Пусть далее для каждого x из сегмента a ≤ x ≤ b существует однократный интеграл

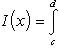
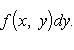(12)

Тогда существует повторный интеграл

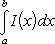
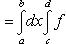
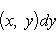
и справедливо равенство

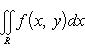
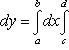
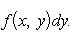(13)

Доказательство. Разобъем прямоугольник R с помощью точек a = x ₀ < x ₁ < x ₂ <... < x_n = b и c = y ₀ < y ₁ < y ₂ <... < y_p = d на n · p частичных прямоугольников

R_kl = [ x_{k -1} ≤ x ≤ x_k ] × [ y_{l -1} ≤ y ≤ y_l ]
(k = 1, 2,..., n; l = 1, 2,..., p).

Положим Δ x_k = x_k - x_{k -1}, Δ y_l = y_l - y_{l -1} и обозначим через M_kl и m_kl точные грани функции f (x, y) на частичном прямоугольнике R_kl. Тогда всюду на этом прямоугольнике

m_kl ≤ f (x, y) ≤ M_kl. (14)

Положим в этом неравенстве x = ξ _k, где ξ _k - произвольная точка сегмента [ x_{k -1}, x_k ], и после этого проинтегрируем (14) по y в пределах y_{l -1} до y_l. Получим

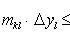
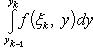
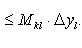(15)

Суммируя (15) по всем l от 1 до p и используя обозначение (12), будем иметь

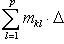
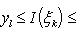
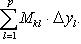(16)

Далее умножим (16) на Δ x_k и просуммируем по всем k от 1 до n. Получим

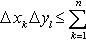
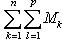
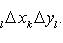(17)

Пусть наибольший диаметр Δ частичных прямоугольников стремится к нулю. Тогда и наибольшая из длин Δ x_k стремится к нулю. Обрамляющие члены в (17), представляющие собой нижнюю и вернюю суммы, стремятся при этом к двойному интегралу .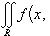

Стало быть, существует предел и среднего члена в (17), равный тому же самому двойному интегралу. Но этот предел по определению однократного интеграла равен

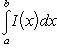
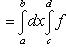
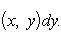
Тем самым доказано существование повторного интеграла и равенство (13). Теорема доказана.

Замечание. В теореме 6 можно поменять x и y ролями, т. е. моно предположить существование двойного интеграла и существование для любого y из сегмента c ≤ y ≤ d однократного интеграла

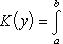
Тогда теорема будет утвердать существование повторного интеграла

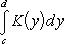
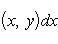
и равенство

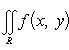
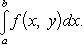(18)