Правила сходимости степенного ряда

Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.

• Первая теорема Абеля: Пусть ряд 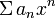сходится в точке 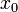. Тогда этот ряд сходится абсолютно в круге 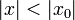и равномерно по на любом компактном подмножестве этого круга.

Обращая эту теорему, получаем, что если степенной ряд расходится при , он расходится при всех , таких что 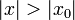. Из первой теоремы Абеля также следует, что существует такой радиус круга (возможно, нулевой или бесконечный), что при 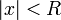ряд сходится абсолютно (и равномерно по на компактных подмножествах круга 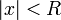), а при — расходится. Это значение называется радиусом сходимости ряда, а круг 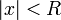— кругом сходимости.

• Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:

Пусть и — два степенных ряда с радиусами сходимост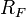и и 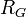. Тогда

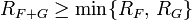
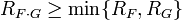
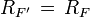
Если у ряда свободный член нулевой, тогда

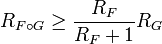
Вопрос о сходимости ряда в точках границы 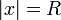круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:

• Признак Д’Аламбера: Если при и 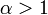выполнено неравенство

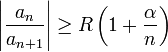
тогда степенной ряд 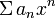сходится во всех точках окружности 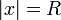абсолютно и равномерно по .

• Признак Дирихле: Если все коэффициенты степенного ряда 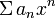положительны и последовательность монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности , кроме, быть может, точки .
• Вторая теорема Абеля: Пусть степенной ряд сходится в точке . Тогда он сходится равномерно по на отрезке, соединяющем точки 0 и .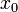

Сумма степенного ряда как функция комплексного параметра является предметом изучения теории аналитических функций.