Замена переменных в двойном интеграле

Для вычисления двойного интеграла иногда удобнее перейти в другую систему координат.
Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции.
В новой системе координат вычисление двойного интеграла значительно упрощается.

Замена переменных в двойном интеграле описывается формулой

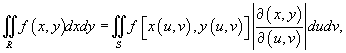
где выражение представляет собой так называемый якобиан преобразования , а S − образ области интегрирования R, который можно найти с помощью подстановки в определение области R. Отметим, что в приведенной выше формуле 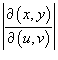означает абсолютное значение соответствующего определителя.

Предполагая, что преобразование координат является взаимно-однозначным, обратное соотношение описывается якобианом

при условии, что знаменатель нигде не равен 0.

Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:

1. Найти образ S в новой системе координат 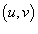для исходной области интегрирования R;

2. Вычислить якобиан преобразования и записать дифференциал в новых переменных ;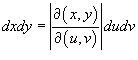

3. Заменить в подынтегральном выражении исходные переменные x и y, выполнив, соответственно, подстановки и .