Уравнение с полным дифференциалом

Пусть имеется дифференцируемая функция двух переменных . Ее дифференциал имеет вид 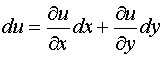. Если известно, что во всей области определения функции , то функция является тождественной константой: . Если же имеется некоторая функция , то, очевидно, что .

Таким образом, если дифференциальное уравнение первого порядка имеет вид

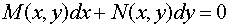, (1)

где 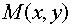, - некоторые функции, то, убедившись, что левая часть уравнения (1) есть дифференциал некоторой функции 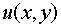, можно записать общий интеграл уравнения

. (2)

Для того, чтобы левая часть уравнения (1) являлась полным дифференциалом некоторой функции необходимо и достаточно, чтобы

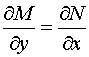, (3)

поскольку если , то , , 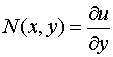а условие (3.3) – не что иное, как равенство .

Так как 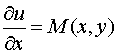, то

. (4)

Функцию 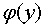найдем, дифференцируя равенство (4) по переменной :

.

Пример 1. Решить дифференциальное уравнение

.

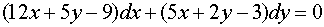Решение. Данное уравнение имеет вид (1), где

, .

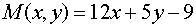Проверим выполнение условия (3):

,

следовательно, данное уравнение есть уравнение в полных дифференциалах. Следовательно,

, ,

,

.

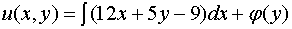Дифференцируем полученное равенство по :

,

откуда .

Решим полученное дифференциальное уравнение

,

Получим .

Общий интеграл уравнения имеет вид

, то есть

.

Если левая часть уравнения (1) не является полным дифференциалом, то можно подобрать (если это удается) функцию 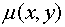, поле умножения на которую левая часть уравнения (1) обращается в полный дифференциал:

. (5)

Функция 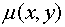называется интегрирующим множителем. Существование интегрирующего множителя было доказано Эйлером, который указал ряд классов дифференциальных уравнений с интегрирующими множителями заданного вида. Надо заметить, что подбор интегрирующего множителя требует некоторой изобретательности.

Пример 2. Решить дифференциальное уравнение

.

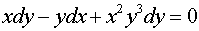Решение. Домножим обе части уравнения на интегрирующий множитель :

,

.

Получили уравнение вида (1), где 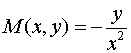, . Проверим выполнение условия (3):

; .

Таким образом, после введения интегрирующего множителя получен полный дифференциал некоторой функции 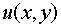, где , .

,

.

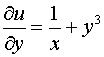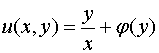Продифференцируем полученное выражение по переменной :

.

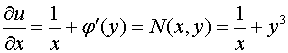Поскольку , то , а искомая функция или .