
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Градиент, дивергенция и ротор
|
|
Важнейшими характеристиками скалярных и векторных полей являются градиент (grad) скалярного поля, дивергенция (div) и ротор (rot) векторного поля.
Определение 3: Градиентом дифференцируемого скалярного поля u(M)=u(x, y, z) называется вектор

Т.е. сумма частных производных умноженных на соответствующие единичные вектора. О производных функии мы писали в предыдущих статьях: Производная функции, Практическое использование понятия: производная функции.
Определение 4: Дивергенцией (или расходимостью) дифференцируемого векторного поля  называется скаляр
называется скаляр

Определение 5: Ротором (или вихрем) дифференцируемого векторного поля  называется вектор
называется вектор
который с помощью символической записи удобно представить в виде векторного произведения
Операторы grad, div, rot называются основными операторами теории поля.
В качестве примеров использования операторов градиента скалярного поля, дивергенции и ротора векторного поля приведем формулу связи напряженности  и потенциала
и потенциала  электростатического поля:
электростатического поля: 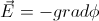 и систему уравнений Максвелла для стационарного электромагнитного поля:
и систему уравнений Максвелла для стационарного электромагнитного поля:
1) 
2) 
3) 
4) 
В математической и особенно физической литературе наряду с введенными операторами широко используется символический векторный дифференциальный оператор набла (оператор Гамильтона). Правила работы с оператором Гамильтона такие же, как и с обычными векторами. Выразим операторы поля через оператор Гамильтона. Вычисляя произведение вектора  на скалярную функцию u, скалярное и векторное произведения вектора
на скалярную функцию u, скалярное и векторное произведения вектора  на вектор
на вектор  , получим формулы
, получим формулы
