
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: похідна та її застосування.
|
|
1.Доведіть тотожність:
 |
Доведення: розглянемо функцію: f (х)= 
f ‘(х)=sin2x(- cos2x + cos2x)
Оскільки, f ‘(х)=0 при будь-яких х, то функція f (х) стала в R.
Знайдемо значення функції в точці х=0.
f(0)=(cos0)4 – 1/8 cos0 – 2(cos0)2 + 1/2cos0=-5/8.
Отже на множині R виконується дана тотожність.
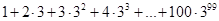 2. Знайдіть суму:
2. Знайдіть суму:
Розв’язання: переформулюємо завдання і знайдемо значення функції f(х)=1+2х+3х2+4х3+…100х99 в точці х=3.
Очевидно f(х)=1+2х+3х2+…+100х99 = (х+х2+х3+…х100)’.
Розглянемо тепер функцію S(х)= х+х2+х3+…х100.
f(х)= S’(х), то f(3)= S’(3).
Доданки функції S(x) утворюють геометричну прогресію, перший член якої х, останній х100, знаменник х.
Функція S (х) – сума геометричної прогресії.
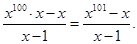 S(х) =
S(х) =
 |
S’(х) =
 | |||
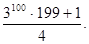 |
f (3)= S’(3)= =
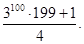 |
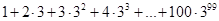 Відповідь: =
Відповідь: =
 3. Порівняйте числа:
3. Порівняйте числа:
Розв’язання: нехай маємо многочлен y = х3 - 6х2 + 9х.
Дослідимо на монотонність:
y’ = 3х2 - 12х + 9
y’ = 0 при х1= 1, х2 = 3
При 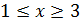 , y’(х)< 0, при х
, y’(х)< 0, при х  3, y’(х)> 0,
3, y’(х)> 0,
Отже y(3, 12341234) < y(3, 12344321), а це означає, що А< В
Відповідь: А< В
 4. Яке з чисел більше:
4. Яке з чисел більше:
Розв’язання: розглянемо функцію f (х) = х+cos х.
Оскільки f ‘(х) = 1-sin х  0 при всіх дійсних х і f’(х)=0 при х=
0 при всіх дійсних х і f’(х)=0 при х= 
Функція f (х) = х+cos х зростає на множині всіх дійсних чисел, тому:
f (1988) < f (1989),
Тобто:
1988+ cos1988< 1989+ cos1989.
Відповідь: cos1988< 1+ cos1989