
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Відповідь: .
|
|
3. Ребро куба ABCDA1B1C1D1 равно a. Найдите расстояние между BD1 и DC1.
Розв’язання: 1. CD 1 – проекція BD 1 на грань CC 1 D 1 D. CD 1 ∩ C 1 D = K (Рис. 10).
2. За теоремою про три перпендикуляри BD 1 ^ C 1 D.
3. В трикутнику BCD 1 опустимо з точки K перпендикуляр KH на сторону BD 1.
4. Відстань між прямими, щоперетинаються дорівнює довжині їх загального перпендикуляра. Площина трикутника BCD1 перпендикулярна C1D, отже відрізок KH перпендикулярний C1D. З іншого боку, KH перпендикулярний BD1 (з побудови). Отже, KH - загальний перпендикуляр для прямих, що перетинаються C1D і BD1, а його довжина і є шукана відстань.
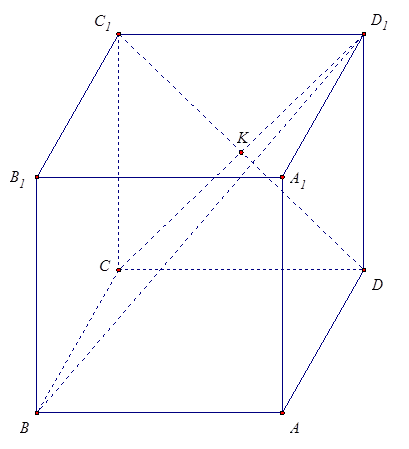
Рис. 10
5. Розглянемо ∆ BCD 1 (чертеж 33). Ð C = 900, BC = a (за умовою), CD 1 = a  (діагональ квадрата зі стороною a), BD 1 = a
(діагональ квадрата зі стороною a), BD 1 = a  (за теоремою Піфагора), KD 1 = ½ CD 1 =
(за теоремою Піфагора), KD 1 = ½ CD 1 =  .
.
6. ∆ BCD 1 ~ ∆ KHD 1 (за двома кутами, (Ð C = Ð H = 900, Ð D 1 – спільний). Тоді  .
.

Рис.11
Отримуємо:  .
.