
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальное уравнение плоскости
|
|
Положение плоскости Q вполне определяется заданием единичного вектора  , имеющего направление перпендикуляра ОК, опущенного на плоскость из начала координат, и длиной р этого перпендикуляра (рис 3).
, имеющего направление перпендикуляра ОК, опущенного на плоскость из начала координат, и длиной р этого перпендикуляра (рис 3).
Пусть ОК=р, а  - углы, образованные единичным вектором
- углы, образованные единичным вектором  с осями Ох, Оу и Oz. Тогда
с осями Ох, Оу и Oz. Тогда  . Возьмем на плоскости произвольную точку
. Возьмем на плоскости произвольную точку  и соединим ее с началом координат. Образуем вектор
и соединим ее с началом координат. Образуем вектор 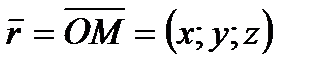 .
.
При любом положении точки М на плоскости Q проекция радиус – вектора 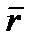 на направление вектора
на направление вектора  всегда равно р:
всегда равно р: 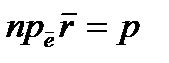 , т.е.
, т.е.  или
или
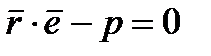 (5)
(5)
Уравнение (5) называется нормальным уравнением плоскости в векторной форме. Зная координаты вектора 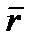 и
и  , уравнение (5) перепишем в виде
, уравнение (5) перепишем в виде
 (6)
(6)
Уравнение (6) называется нормальным уравнением плоскости в координатной форме.
Отметим, что общее уравнение плоскости (2) можно привести к нормальному уравнению (6), а именно умножить обе части уравнения (2) на нормирующий множитель  , где знак берется противоположным знаку свободного члена D общего уравнения плоскости.
, где знак берется противоположным знаку свободного члена D общего уравнения плоскости.