
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма.
|
|
Цель занятии: Решение задач статистическим методом обработки экспериментальных данных
Вопросы: Эмпирическая функция распределения. Полигон и гистограмма. Интервальные оценки.
Статистическим распределением выборки называют перечень вариант хi вариационного ряда и соответствующих им частот пi (сумма всех частот равна объем выборки п) или относительных частот  (сумма относительных частот равна единице).
(сумма относительных частот равна единице).
Примери1. Выборка задана в виде распределения частот:

Найти распределение относительных частот.
Решение. Найдем объем выборки п=1+3+6=10. Найдем относительные частоты:

Напишем искомое распределение относительных частот.

Контроль: 0, 1+0, 3+0, 6=1.
Пример 2. Найти эмпирическую функцию по данному распределению выборки:

Решение: Найдем объем выборки: п=10+15+25=50.
Наименьшая варианта равна единице, поэтому  при
при  .
.
Значение 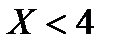 , а именно
, а именно  , наблюдалось 10 раз, следовательно,
, наблюдалось 10 раз, следовательно,  при
при  .
.
Значения  , а именно:
, а именно:  и
и  , наблюдались 10+15=25 раз; следовательно,
, наблюдались 10+15=25 раз; следовательно,  при
при  .Так как х=6-наибольшая варианта, то
.Так как х=6-наибольшая варианта, то  при
при  .
.
Напишем искомую эмпирическую функцию: 
Пример 3. Построить полигон частот по данному распределению выборки:

Решение: Отложим на оси абсцисс варианты хi, а на оси ординат –соответствующие им частоты пi –соединив точки (хi,, пi) отрезками прямых, получим искомый полигон частот.
Рекомендуемая литература: ОЛ [7], [10]