Основные соотношения и свойства модели межотраслевого баланса

Рассматривается, в соответствии с [51, 1], экономика региона, имеющая n отраслей. Каждая отрасль выпускает продукт, часть которого потребляется другими отраслями (промежуточный продукт) – представлен в первом квадранте, а вторая часть идет на потребление и накопление (конечный продукт)– во втором квадранте. Денежный доход от производства продукции – представлен в третьем квадранте.

Обозначим:

X_i – валовой объем выпуска продукции i-ой (производящей) отрасли;

x_ij – стоимость продукции произведенной i-ой отраслью, идущей на производство j-ой отрасли, т. е. для j-ой отрасли x_ij – это затраты, которые она использует для изготовления своей продукции стоимостью X_j - потребляющей отрасли;

y_i - конечный продукт i-ой отрасли;

z_j – денежный доход от производства продукции j-ой отрасли, включающей в себя заработанную плату, налоги, амортизацию прибыль и пр.

Валовой объем выпуска производящей отрасли равен сумме стоимостей продукции произведенной этой отраслью и переданной (проданной) во все отрасли и конечной продукцией отрасли: X_i= + +…+ +y_i или

X_i= + y_i, i= . (12.6.1)

Уравнения (12.6.1) называются балансами «выпуска».

Валовой объем выпуска потребляющей отрасли равен сумме материальных затрат на производимую продукцию в других отраслях и денежный доход от производства продукции:

X_j= 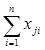+ z_j, j= . (12.6.2)

Уравнения (12.6.2) называются балансами «затрат».

А в совокупности уравнения (12.6.1), (12.6.2) называются моделью «затраты - выпуск».

Из анализа (12.6.1) вытекает, промежуточное потребление (затраты) зависят от объема производимой продукции X_j – чем больше выпуск отрасли X_j, тем больше затраты .

В базовой модели межотраслевого баланса используется допущение о пропорциональной зависимости между затратами j-ой отрасли и объемом ее производства, т.е. вводятся линейные однородные функции производственных затрат j-ой отрасли:

x_ij = a_ijX_j, (12.6.3)

где X_j - объем производства j-ой отрасли; a_ij– коэффициент пропорциональности – определяет прямые затраты.

Коэффициент прямых затрат:

a_ij= ³ 0, (12.6.4)

показывает, какое количество продукции i-ой отрасли необходимо для производства единицы продукции j-ой отрасли. Эти коэффициенты в совокупности образуют квадратную матрицу n-го порядка: A={a_ij, i, j= }.

Подставив значения a_ij из выражения (12.6.3) в выражение (12.6.1), получим систему алгебраических уравнений с 2n переменными X_i и y_i.

X_i= 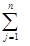a_ijX_j + y_i, i = , (12.6.5)

или 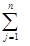(I_ij - a_ij)X_j = y_i, i = ,

где I_ij - элемент единичной матрицы:

I_ij = .

В векторно-матричной форме имеем:

X = AX + Y, или (I - A)X = Y, (12.6.6)

где X={X_j, j= } - вектор-столбец валовых выпусков; Y={y_i, i= } - вектор-столбец конечной продукции; I - единичная матрица.

Уравнения (12.6.6) представляют модель Леонтьева " затраты - выпуск", или уравнения межотраслевого баланса.

Пример 2. Расчет коэффициентов прямых затрат - представлен в 13.5.

Система уравнений МОБ может иметь единственное решение, если из общего количества величин x_i и y_i число неизвестных не превышает числа уравнений (необходимое, но не достаточное условие). Принятие одних величин за известные (экзогенные), а других за неизвестные (эндогенные) определяется постановкой экономической задачи. Главное достоинство модели - возможность проведения многовариантных аналитических и прогнозных расчетов с меняющимися значениями x_i и y_i. Основное допущение состоит в том, что коэффициенты a_ij принимаются неизменными в рамках изучаемого периода.

Свойства решений системы уравнений МОБ определяется свойствами матрицы А.

Матрица коэффициентов прямых материальных затрат А относится к классу неотрицательных матриц a_ij> 0, " i, jÎ n. Но коэффициенты матрицы А не могут принимать произвольные положительные значения. Например, все диагональные элементы должны быть меньше единицы, также меньше единицы должны быть произведения коэффициентов, симметричных относительно главной диагонали (a_lka_kl< 1). Главным обобщающим свойством матрицы А является продуктивность.

Матрица А называется продуктивной, если существует неотрицательный вектор Х 0, позволяющий получить положительный вектор конечного спроса: (I-A)X = Y > 0. Достаточным условием продуктивности является выполнение соотношений a_ij < 1 для всех j = .

Пример 3. Расчет суммы коэффициентов прямых материальных затрат в матрице межотраслевого баланса Приморского края.

Основная теорема для модели межотраслевых материальных связей:

если матрица А продуктивна, то для любого полуположительного вектора Y 0 (т. е. имеющего хотя бы одну положительную компоненту) система (I-A)X=Y имеет единственное полуположительное решение Х 0.

Из модели Леонтьева " затраты - выпуск" вытекает два тождества. Первое следует из уравнений (12.6.1), (12.6.2):

+ y_i= 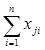+ z_j, i= .

Эти уравнения означают, что производственные (материальные) затраты i-ой отрасли, увеличенные на добавленную стоимость выпускаемой ею продукции, равны стоимости выпуска этой отрасли.

Просуммируем уравнения (12.6.7) по i= отраслям

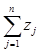+ = + . (12.6.7)

Первые слагаемые этих уравнений равны: = ,

отсюда = .

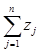Равенство означает, что общая сумма конечных спросов равна общей сумме добавленных стоимостей. Систему матричных уравнений можно представить в виде:

X = (I - A)^-1Y, (12.6.8)

где (I - A)^-1 - квадратная матрица n-го порядка, обратная (I-A).

Обозначим B = (I - A)^-1. B ={b_ij, i, j= },

где b_ij – коэффициенты пропорциональности, определяющие полные затраты.

Коэффициент полных затрат - b_ij, образующих матрицу B, показывает какое количество продукции i-ой отрасли необходимо произвести, чтобы с учетом прямых и косвенных затрат этой продукции, получить единицу конечной продукции j-ой отрасли. Действительно, предположим, что вектор конечного спроса имеет следующую размерность: Y={y₁=0, y₂=0, …,, y_j-1=0, y_j=1, y_j+1=0, …, y_n=0}, тогда подставляя его в (12.6.7), получим X_j=b_ij. Отсюда, b_ij – это количество валовой продукции отрасли i, необходимой для выпуска единицы конечной продукции (в стоимостном выражении) отрасли j.

Коэффициенты b_ij дают ценную информацию о структурных зависимостях между компонентами конечного спроса (потребление, накопление, вывоз т. д.) и необходимыми для их обеспечения объемами выпусков.

Доказывается, что b_ij a_ij, а диагональные элементы b_ij 1+a_ij. В целом B=(I - A)^-1 - это матричный мультипликатор совокупного регионального продукта по отношению к конечному продукту региона.

Пример 4. Расчет матрицы коэффициентов полных затрат.