Учет производственных ресурсов и мощностей в модели межотраслевого баланса

Возможности увеличения производства каждой отрасли ограничены имеющимися ресурсами, не восполняемыми в каждом выбранном промежутке времени. Если рассматривать годовой цикл, то не восполняемыми (ограниченными) следует считать природные и трудовые ресурсы. Ограниченными будут также ресурсы основного производственного капитала (производственные мощности).

Распространив предположение о пропорциональности затрат и объемов производства на множество ограниченных ресурсов, получим дополнительную систему линейных неравенств:

r_ojx_j b_o, o= , (12.6.9)

где r_oj - прямые затраты r-го ресурса, идущего на производство единицы продукции отрасли O, О – множество видов деятельности на уровне разделов и подразделов, в соответствии с ОКВЭД; b_o - имеющейся объем o-го ресурса на исследуемый период планирования.

В векторно-матричной форме условия (12.6.8) примут вид:

RX B, (12.6.10)

где R - матрица ресурсных коэффициентов, B - вектор имеющихся ресурсов.

По этой формуле исчисляются полные затраты труда, основного капитала и других производственных ресурсов.

Пример 5. Расчет полных затрат труда в межотраслевом балансе.

Особым видом ресурсов являются наличные производственные мощности по видам продукции (М_j), характеризующие максимально возможные выпуски продукции за год. Ограничения на имеющиеся мощности учитываются в модели МОБ следующим образом:

X_j М_j, j= , (12.6.11)

или X М, (12.6.12)

где М = {М_j, j= } - вектор-столбец производственных мощностей.

Соответственно, (I - A)^-1Y М, (12.6.13)

Подключим ограничения по производственным ресурсам и мощностям к системе уравнений материального МОБ:

(I - A)X=Y, (12.6.14)

RX B, (12.6.15)

X_j М_j, j = . (12.6.16)

Решение этой системы означает, что допустимыми могут являться только такие векторы Х, Y, которые удовлетворяют условиям (12.6.14)-(12.6.15).

Используя информацию зависимости выпусков отраслей и затрат производственных ресурсов от отраслевой структуры конечного спроса (12.6.8) можно определить распределение выпуска X на обеспечение конечного спроса отраслей Y={y_i, i = }.

Допустим, что отраслевая структура совокупного конечного спроса зафиксирована, то общий объем конечного спроса: y= 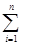a_iy_i, где a=(a_i, i= ) - вектор-столбец отраслевой структуры конечного спроса в сумме равные единице, т.е. 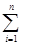a_i=1. Отсюда, взаимосвязь выпуска от отраслевой структуры конечного спроса (12.6.8) представим в виде выражения:

X = (I - A)^-1ay = by, (12.6.17)

где b = (I - A)^-1a - вектор-столбец выпусков отраслей, необходимых для получения общего объема конечного спроса.

Пример 6. Распределение выпуска на обеспечение конечного спроса отраслей.

Аналогично можно определить потребность в трудовых ресурсах на единицу общего объема конечного спроса:

g = Ta, (12.6.18)

где Т - вектор-строка затрат трудовых ресурсов по отраслям. (См. последнюю строку рис. 13.1).

Пример 7. Потребность в трудовых ресурсах на единицу общего объема конечного спроса.

Проанализируем теперь зависимости выпусков и затрат производственных ресурсов от функциональной структуры конечного спроса.

ПустьY={Y_s, s= }, - вектор-столбец s-й функциональной части конечного спроса (S – множество частей конечного спроса: конечное потребление, в т. ч. расходы домохозяйств и государственные расходы; валовое накопление, в т. ч. инвестиции в основной капитал, сальдо вывоза (экспорт) и ввоза (импорт) и т. д.);

X_s - вектор-столбец выпусков, необходимых для получения Y_s;

Q_s - вектор-столбец производственных ресурсов, необходимых для получения Y^s.

Очевидно, что

X_s = (I - A)^-1 Y_s, (12.6.19)

Q_s = FY_s, s= ,

X = 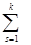X_s, Q = 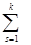Q_s.

Пример 8. Оценка последствий изменений функциональной структуры конечного спроса

Выведенные соотношения могут использоваться в экономической политике для оценки последствий изменений функциональной структуры конечного спроса. В частности, а) если признается целесообразным увеличить долю накопления, то можно ожидать увеличение спроса на продукцию ряда отраслей и рост валового выпуска, б) если же увеличивается доля конечного потребления, то следствием этого может стать рост выпуска и увеличение занятости.