
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение агрегированной модели трехуровневой ИС: предприятие - отрасли - регион и ее решение.
|
|
13.2.1. Введение.
При формировании годовых пятилетних планов предприятий обычно исследуется от нескольких сот до нескольких тысяч изделий и, если учесть, что в отрасли находится до нескольких десятков предприятий, то понятно, что задача (13.1.1)-(13.1.7) имеет очень большой объем информации и решение ее «в лоб» не представляется возможным. Для уменьшения объема информации, обрабатываемой в модели (13.1.1)-(13.1.7), при переходе от уровня предприятия к уровню отрасли и от уровня отрасли к уровню региона используем композиционные и декомпозиционные методы последовательного агрегирования информации разработанных в [1, 2].
13.2.2. Агрегирование информации в математической модели: отрасль - предприятия
Для упрощения дальнейших вычислений выделим из модели (13.1.1)-(13.1.7) двухуровневую ИС отрасль - предприятия:
Opt Fo(Xo(t))={opt F1o(Xo(t)) = {fкп (Xп(t)), к=  п, п=
п, п=  o}, (13.2.1)
o}, (13.2.1)
opt F2o(Xo(t))={fко(Xo(t))= 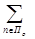 fкп(Xп(t)), к=
fкп(Xп(t)), к=  o, Ko=
o, Ko=  Kп }}, (13.2.2)
Kп }}, (13.2.2)
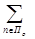
 aijxj(t) £ bi, i Î Mo, (13.2.3)
aijxj(t) £ bi, i Î Mo, (13.2.3)
 aijxj(t) £ bi, i Î Mп, п=
aijxj(t) £ bi, i Î Mп, п=  o, (13.2.4)
o, (13.2.4)
xj(t) £ uj(t), j=  п, п=
п, п=  o, " oÎ Or, " rÎ R. (13.2.5)
o, " oÎ Or, " rÎ R. (13.2.5)
Обозначения аналогичные, как и в модели (13.1.1)-(13.1.7).
Агрегирование информации в модели (13.2.1)-(13.2.5) возможно при условии, что все предприятия, входящие в отрасль, должны иметь соизмеримые критерии (например, объемы продаж, прибыль, товарная и валовая продукция и т.п. для машиностроительных отраслей; объем строительно-монтажных работ, ввод основных фондов, капитальных вложений и т.п. для строительной отрасли и т.д.).
Предполагается, что выполняются основные условия агрегации [2], при этом несколько критериев (как минимум один) для всех предприятий входящих в отрасль oÎ Or в (13.2.1)-(13.2.5), должны обладать свойством аддитивности, т.е. критерии различных предприятий могут складываться, сохраняя технико-экономическую сущность показателя. Один из таких критериев назовем ведущим критерием.
Далее представим описание в соответствии с методикой (см. 5.6.2) в [2]
Шаг 1. Пусть в ВЗЛП (13.2.1)-(13.2.5) для всех предприятий ведущим критерием будет vÎ K - объемы продаж, получаемые от производства Хп , " пÎ Пo, " oÎ Or объемов продукции.
Шаг 2. Решим ВЗЛП (13.2.1)-(13.2.5) для всех предприятий. в результате получим, что ведущий критерий fv(Х*) для каждого предприятия лежит в пределах от величины fv(Хoп), полученной при равнозначных критериях, до fv(Х*), полученной при решении ВЗЛП по одному критерию vÎ K, т.е.
fv(Хпo(t)) £ fv(Хп(t)) £ fv(Х*(t)), (13.2.6)
остальные критерии и ограничения определяются аналогично:
fкп(Хoп(t)) £ fкп (Хп(t)) £ fкп(Х*(t)), kÎ K (13.2.7)
AiХoп (t) £ AiХп(t) £ AiХ*(t), iÎ M. (13.2.8)
Шаг 3. Представим ведущий критерий fv(Хп(t)) одной переменной yп=fv(Хп(t)), тогда обозначая yoп(t)= fkп(Xoп(t)), y*п(t)=fп(Х*п(t)), соотношения (13.2.8) примут вид yoп(t) £ yп(t) £ y*п(t).
Примечание. Представление ведущего критерия fv(Хп(t)) одной переменной это частный случай общего подхода, когда ведущий критерий fv(Хп(t)) может быть представлен двумя, тремя и т. д. количеством переменных.
Шаг 4, 5. Предполагая линейную функциональную зависимость между ведущим критерием и остальными критериями и ограничениями при оптимизации, преобразуем их:
fkп(Хoп(t)) £ cokп +ckпyп (t)£ fкп(Х*(t)), (13.2.9)
АiXoп (t)£ aoiп+aiпyп(t) £ AiX*(t), iÎ M. (13.2.10)
Расчет аппроксимационных коэффициентов см. раздел 5.6.
Шаг 6. С учетом введенных обозначений (13.2.9)-(13.2.10), преобразуем модель отдельного предприятия, входящую составной частью в ИС отрасль - предприятия (13.2.1)-(13.2.5) и имеющую Nп переменных Xп(t)={xj(t), j=  п}, в векторную задачу, имеющую одну переменную Yп(t) ={yn(t), " пÎ П o}:
п}, в векторную задачу, имеющую одну переменную Yп(t) ={yn(t), " пÎ П o}:
opt fkп(Xп(t)) Û opt fkп(Yп(t) ={
{opt f1vп(Yп(t)) =yn(t), vÎ K}, (13.2.11)
{opt f2kп(Yп(t) =coko+ckn yn(t)), к=  п }}, (13.2.12)
п }}, (13.2.12)
(a0in+ain yn(t)) £ bi , iÎ M, (13.2.13)
(a0in + ain yn(t)) £ Ri, iÎ M, (13.2.14)
yno(t) £ yn(t) £ yn*(t), " пÎ П o, " oÎ O, (13.2.15)
где соотношение opt fkп(Xп(t)) Û opt fkп(Yп(t) показывает, что векторный критерий fkп(Xп(t)), описывающий функционирование п-го предприятия и взятый из (13.2.1), эквивалентен fkп(Yп(t) - агрегированному векторному критерию, каждая компонента которого функционально зависит от агрегированного вектора переменных Yп(t) ={yn(t)}, " пÎ Пo, " oÎ O, (в нашем случае вектор Yп(t) состоит из одной компоненты, в общем случае таких компонент может быть любое количество и оно определено на шаге 3). Эквивалентность критериев (знак Û) говорит о том, что количество компонент у них одинаково, а их величина отличается друг от друга соответственно на величину равную ошибке аппроксимации (подробнее см. в [2]);
агрегированный векторный критерий fkп(Yп(t)) состоит из дух подмножеств - первое (13.2.11) представлено одной компонентой, а второе (13.2.12) остальными компонентами множества Kп, " пÎ П o, " oÎ O;
аналогично для ограничений:
ограничениям (13.2.4) эквивалентен их агрегированный вариант (13.2.15), а для ограничений (13.2.5) эквивалентен их агрегированный вариант (13.2.14):
для вектора переменных представленного соотношениями (13.2.5) эквивалентен агрегированный вектор (13.2.15).
Переменную yn(t), пÎ Пo, " oÎ O можно трактовать как агрегированный продукт, каждая единица которого приносит один рубль дохода предприятию, полученный в период tÎ T.
Шаг 7. (Аналогичен шагу 1 блока 2, см. раздел 5.6 в [2]). В целом задачу отрасль-предприятие, представленную моделью (13.2.1)-(13.2.7), объединяя все агрегированные модели (13.2.11)-(13.2.15) можно представить в агрегированном виде: opt Fo(Xo(t)) Û opt Fo(Yo(t)) ={
opt F1o(Yo(t))={fvп(Yп(t))=yn(t), vÎ Kn, п=  o}, (13.2.16)
o}, (13.2.16)
opt F2o(Yo(t))={fko(Yo(t))= 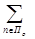 (coko+ckn yп(t)), к=
(coko+ckn yп(t)), к=  o}}, (13.2.17)
o}}, (13.2.17)
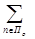 (aoin+ain yn(t)) £ bi , iÎ M, (13.2.18)
(aoin+ain yn(t)) £ bi , iÎ M, (13.2.18)
yno(t) £ yn(t)£ yn*(t), п=  o, " oÎ O, (13.2.19)
o, " oÎ O, (13.2.19)
где соотношение opt Fo(Xo(t)) Û opt Fo(Yo(t)) показывает эквивалентность векторного критерия (13.2.1), имеющего переменную Xo(t) размерностью Nn*П o, " oÎ O и агрегированного векторного критерия Fo(Yo(t)), полученного из объединения (13.2.11) и имеющего переменную Yo(t) размерностью 1*П o, " oÎ O;
агрегированный векторный критерий Fo(Yo(t)) состоит из двух подмножеств - первое (13.2.16) представлено от каждого предприятия одной компонентой {yn(t), п=  o}, каждое из которых являются агрегированным ведущим критерием предприятия, - второе F2о(Yo(t)) = {fko(Yo(t)), k=
o}, каждое из которых являются агрегированным ведущим критерием предприятия, - второе F2о(Yo(t)) = {fko(Yo(t)), k=  o, Ko=
o, Ko=  Kп } - векторный отраслевой критерий, каждая компонента которого представляет сумму отдельных критериев предприятий, обладающих свойствами аддитивности, и, в частности, одним их таких критериев может быть сумма объема продаж по всем предприятиям отрасли: fvo(Yo(t)) =
Kп } - векторный отраслевой критерий, каждая компонента которого представляет сумму отдельных критериев предприятий, обладающих свойствами аддитивности, и, в частности, одним их таких критериев может быть сумма объема продаж по всем предприятиям отрасли: fvo(Yo(t)) = 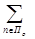 yn(t), " oÎ O;
yn(t), " oÎ O;
(13.2.18) - агрегированные ограничения по ресурсам, они эквивалентны ограничениям (13.2.4) и составлены суммированием (13.2.13);
для агрегированного вектора переменных представленного соотношениями (13.2.19) эквивалентными являются (13.2.5).
Шаг 8. (Аналогичен шагу 2 блока 2, см. раздел 5.6 в [2]). Решается ВЗЛП (13.2.16)-(13.2.19) при равнозначных критериях.
В результате решение задачи (13.2.16)-(13.2.19) на планируемый год tÎ T получим: точку оптимума Yoo(t)={yno(t), п=  o} и максимальную относительную оценку lo(t), такую, что
o} и максимальную относительную оценку lo(t), такую, что
lo(t)=lп(yno(t)), п=  o, (13.2.20)
o, (13.2.20)
для критерия (13.2.16), т. к. критерии независимы; и
lo(t) £ lk (yno(t)), k=  o, (13.2.21)
o, (13.2.21)
для критерия (13.2.17), т.е. lo(t) является максимальным нижним уровнем для всех относительных оценок lk(X(t)), k=  или гарантированным результатом в относительных единицах, а в соответствии с теоремой 3, точка {Yo, lo } оптимальна по Парето. (В обозначении Yoo(t) верхний индекс читается как «нулевое», в соответствии с результатом решения ВЗЛП в главах 2, 3, а нижний как «о» - отрасль).
или гарантированным результатом в относительных единицах, а в соответствии с теоремой 3, точка {Yo, lo } оптимальна по Парето. (В обозначении Yoo(t) верхний индекс читается как «нулевое», в соответствии с результатом решения ВЗЛП в главах 2, 3, а нижний как «о» - отрасль).
Полученная точка оптимума Yoo(t)={yno(t), п=  o} определяет агрегированный вид продукции, выпускаемой каждым предприятием, и соответствующие технико-экономические показатели, включенные в план.
o} определяет агрегированный вид продукции, выпускаемой каждым предприятием, и соответствующие технико-экономические показатели, включенные в план.
Подставляя значения yno(t), " пÎ По в критерии (13.2.18) и ограничения (13.2.20) в отраслевом разрезе получим информационную модель - Im предприятия на планируемый год tÎ T: Im п(t)={ yno(t), fk(yno(t))=  cjk yjo(t), k=
cjk yjo(t), k=  п ,
п ,
Gi(yno(t)), i= 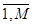 o, o=
o, o=  , i=
, i= 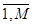 tr, i=
tr, i= 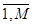 f}, " пÎ Пo, " oÎ O. (13.2.22)
f}, " пÎ Пo, " oÎ O. (13.2.22)
Объединяя все Im предприятий на планируемый год tÎ T получим агрегированную Im отрасли:
Im о(t)={ Yoo(t)={yno(t), п=  o}, fk(Yoo(t))=
o}, fk(Yoo(t))= 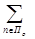 cпk yno(t), k=
cпk yno(t), k=  o, Ko=
o, Ko=  Kп, Gi(Yoo(t)), i=
Kп, Gi(Yoo(t)), i= 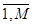 o, o=
o, o=  , i=
, i= 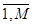 tr, i=
tr, i= 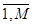 f}, " oÎ O. (13.2.23)
f}, " oÎ O. (13.2.23)
При решении ВЗЛП (13.2.16)- (13.2.19) на период tÎ T лет получим развитие отрасли в динамике в виде набора Im на каждый период планирования.
13.2.3. Агрегирование информации модели: регион - отрасли.
Математические модели, описывающие функционирование отраслей и региона в из взаимосвязи, предназначены, прежде всего, для изучения общих тенденций развития экономики региона, закономерностей его расширенного воспроизводства, роста его национального дохода, исследования межотраслевых пропорций и влияния отраслей друг на друга при их динамическом развитии.
При рассмотрении следующего уровня в ВЗЛП (13.1.1)-(13.1.9) выделяем двухуровневую экономическую систему, высшей управляющей подсистемой которой является орган, моделирующий экономическую деятельность региона и o=  локальных подсистем, моделирующих деятельность отраслей региона. Модель регион - отрасли (13.1.1)-(13.1.9) с учетом моделей (13.2.18)-(13.2.22) представим в агрегированном виде:
локальных подсистем, моделирующих деятельность отраслей региона. Модель регион - отрасли (13.1.1)-(13.1.9) с учетом моделей (13.2.18)-(13.2.22) представим в агрегированном виде:
opt Fr(Xr(t)) Û opt Fr(Yr(t))={opt F1r(Yr(t))=
{fko(Yo(t))= 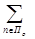 (cokп+ckn yп(t)), к=
(cokп+ckn yп(t)), к=  o, o=
o, o=  r}, (13.2.27)
r}, (13.2.27)
opt F2r(Yr(t))={fк(Yr(t)) =  fко(Yo(t)), к=
fко(Yo(t)), к=  r, Kr=
r, Kr= 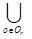 Ko }}, (13.2.28)
Ko }}, (13.2.28)
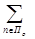 (aoin+ain yn(t)) £ bi , iÎ M, (13.2.29)
(aoin+ain yn(t)) £ bi , iÎ M, (13.2.29)
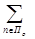 (aoin + ain yn(t)) £ Ri, iÎ M, (13.2.30)
(aoin + ain yn(t)) £ Ri, iÎ M, (13.2.30)
yno(t) £ yn(t)£ yn*(t), п=  o, o=
o, o=  r, " rÎ R, (13.2.31)
r, " rÎ R, (13.2.31)
В данной модели в качестве переменной взят вектор Yr(t) ={Yо(t)= {yn(t), п=  o}, o=
o}, o=  r} " rÎ R - определяющий агрегированные объемы продукции, выпускаемой регионом и его отраслями.
r} " rÎ R - определяющий агрегированные объемы продукции, выпускаемой регионом и его отраслями.
Соотношение opt Fr(Xr(t))Û opt Fr(Yr(t)) показывает эквивалентность векторного критерия (13.1.1), имеющего переменную Xr(t) размерностью Nn*Пo*Or, " rÎ R и агрегированного векторного критерия Fr(Yr(t)), полученного из объединения (13.2.19) с переменной Yr(t) размерностью 1*П o*Or, " rÎ R;
агрегированный векторный критерий Fr(Yr(t)) состоит из двух подмножеств: первое (13.2.27) представляет цель каждой отрасли и определяется множеством критериев
fко(Yo(t))= 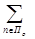 cкпfкп(yп(t)), к=
cкпfкп(yп(t)), к=  o, Ko=
o, Ko=  Kп, o=
Kп, o=  r, (13.2.32)
r, (13.2.32)
которые функционально взаимно связаны с объемами продукции, выпускаемых своими предприятиями, а в соответствии с агрегацией проведенной в предыдущем разделе в каждый из них входит лишь п=  o переменных, т.е. равно количеству предприятий, входящих в отрасль;
o переменных, т.е. равно количеству предприятий, входящих в отрасль;
второе F2r(Yr(t))={  fко(Yo(t)), к=
fко(Yo(t)), к=  r, Kr=
r, Kr= 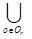 Ko } - векторный критерий региона, каждая компонента которого представляет сумму отдельных критериев отраслей, обладающих свойствами аддитивности.
Ko } - векторный критерий региона, каждая компонента которого представляет сумму отдельных критериев отраслей, обладающих свойствами аддитивности.
Деятельность региона ограничена имеющимися у него ресурсами (бюджет, дефицитные ресурсы) - (13.2.29)-(13.2.31):
(13.2.29) - агрегированные ограничения по ресурсам, они эквивалентны ограничениям (13.1.4) и составлены суммированием (13.2.20);
(13.2.30) - затраты по ресурсам, которые определяют отраслевые затраты на управленческую деятельность, они эквивалентны ограничениям (13.1.6) и составлены суммированием (13.2.21);
для агрегированного вектора переменных представленного соотношениями (13.2.31) эквивалентными являются (13.1.9).
Построение агрегированной модели отрасли.
Цель отрасли состоит в определении вектора Yо(t)= {yn(t), п=  o, " oÎ O, который оптимизировал свою компоненту критерия (13.2.27), при этом каждая отрасль стремится получить как можно больше ресурсов региона, тем самым осуществляется межотраслевая конкуренция.
o, " oÎ O, который оптимизировал свою компоненту критерия (13.2.27), при этом каждая отрасль стремится получить как можно больше ресурсов региона, тем самым осуществляется межотраслевая конкуренция.
При построении агрегированной модели отрасли предполагается, что выполнены основные условия агрегации (см. раздел 5.6). В качестве ведущего критерия и соответственно переменной zo, " oÎ O примем совокупный конечный продукт отрасли, определяемый суммарным агрегированным продуктом всех предприятий входящих в отрасль:
zo= 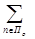 (cokп+ckn yп(t), " oÎ O. (13.2.33)
(cokп+ckn yп(t), " oÎ O. (13.2.33)
При решении ВЗЛП (13.2.27)-(13.2.31) легко вычислить, что агрегированная переменная zo, " oÎ O лежит в пределах
0 £ zo £ zo*, " oÎ O.
Тогда, опуская шаги 2-5 и используя ограничение по агрегированному продукту каждой отрасли, построим модель отрасли в виде ВЗЛП:
opt Fo(Xo(t)) Û opt Fo(Yo(t) Û opt Fo(Zo(t))={
opt F1vo(Zo(t))={zo(t), vÎ Ko}, (13.2.34)
opt F2ko(Zo(t))={(cko zo(t)), к=  o}}, (13.2.35)
o}}, (13.2.35)
aio zo(t) £ bi , iÎ M, (13.2.36)
aio zo(t) = Ri, iÎ Mo, (13.2.37)
0 £ zo(t) £ zo*(t), " oÎ O, (13.2.38)
где соотношение opt Fo(Xo(t))Û opt Fo(Yo(t)Û opt Fo(Zo(t)) показывает двойную эквивалентность (двойную агрегацию) векторного критерия отрасли (13.2.1), имеющего переменную Xo(t) размерностью Nn*Пo, " oÎ O, агрегированного векторного критерия Fo(Yo(t)), с переменной Yo(t) размерностью 1*П o, " oÎ O, рассмотренного в модели (13.2.18)-(13.2.22) и агрегированного векторного критерия Fo(Zo(t)), с переменнуой Zo(t) размерностью 1;
агрегированный векторный критерий Fo(Zo(t)) состоит из двух подмножеств - первое (13.2.34) представлено одной компонентой vÎ Ko, являющейся агрегированным ведущим критерием отрасли, - второе представлено F2ko(Zo(t))- векторным критерием, количество компонент которого определено остальными компонентами множества Ko, " oÎ O;
ограничениям (13.2.20) эквивалентен их агрегированный вариант (13.2.36), а для ограничений (13.2.21) эквивалентен вариант (13.2.37);
для вектора переменных представленного соотношениями (13.2.22) эквивалентен агрегированный вектор (13.2.38).
Переменную zo(t), oÎ O можно трактовать как агрегированный совокупный продукт отрасли, каждая единица которого приносит один рубль дохода, полученного в период tÎ T.
Для любого фиксированного tÎ T вектор-столбец (13.2.34)-(13.2.38) представляет планируемую информационную модель отрасли, аналогично (13.2.26).
Построение агрегированной модели региона.
Введем некоторые обозначения, которые обычно используются в межотраслевом балансе:
xij(t) - объемы продукции (агрегированной) i-ой отрасли, затраченные в j-ой. Используя (13.2.37), xij(t) можно представить:
xij(t) = aio zo(t), i=  , " oÎ O. (13.2.39)
, " oÎ O. (13.2.39)
где aio - коэффициенты прямых затрат, определяющие, какое количество продукта i-ой отрасли необходимо истратить на производство единица продукции о-ой отрасли.
Переобозначим совокупный продукт i-ой отрасли xi(t), i=  . Тогда, суммируя все агрегированные затраты продукции этой отрасли (13.2.39) по всем отраслям, получим совокупный продукт i-ой отрасли.
. Тогда, суммируя все агрегированные затраты продукции этой отрасли (13.2.39) по всем отраслям, получим совокупный продукт i-ой отрасли.
xi(t)=  xij(t)+yi(t), " iÎ O,
xij(t)+yi(t), " iÎ O,
где yi - конечный продукт i-ой отрасли. Подставляя (13.2.39) получим:
xi(t)=  aij xi(t) +yi(t), " iÎ O. (13.2.40)
aij xi(t) +yi(t), " iÎ O. (13.2.40)
Такие i=  , уравнений определяют межотраслевой баланс региона в агрегированном виде.
, уравнений определяют межотраслевой баланс региона в агрегированном виде.
В качестве ведущего критерия и соответственно переменной примем конечный агрегированный продукт отрасли, который может быть вычислен из (13.2.40), и обозначим его индексом oÎ O: yo(t)=xo(t)-  ajo xo(t), " oÎ O.
ajo xo(t), " oÎ O.
Используя полученное соотношения для всех отраслей региона o=  r, " rÎ R, агрегированную модель отрасли (13.2.34)-(13.2.38), и вычисления, полученные на шаге 2-5, преобразуем модель системы регион - отрасли (13.2.27)- (13.2.31) в агрегированную модель:
r, " rÎ R, агрегированную модель отрасли (13.2.34)-(13.2.38), и вычисления, полученные на шаге 2-5, преобразуем модель системы регион - отрасли (13.2.27)- (13.2.31) в агрегированную модель:
opt Fr(Xr(t)) Û opt Fr(Yr(t)) Û opt Fr(Zr(t)) «opt Fr(Yr(t)=
{opt F1r(Yr(t))={fo(Yo(t))= yo(t)), o=  r }, (13.2.41)
r }, (13.2.41)
{opt F2r(Yr(t))={fк(Yr(t))=  fко(Yo(t)), к=
fко(Yo(t)), к=  r, Kr=
r, Kr= 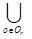 Ko}}, (13.2.42)
Ko}}, (13.2.42)
yo (t)= xo(t)-  aio xo(t), o=
aio xo(t), o=  r, (13.2.43)
r, (13.2.43)
 (aio xo(t)) £ bi, iÎ M, M=MTÈ MF, (13.2.44)
(aio xo(t)) £ bi, iÎ M, M=MTÈ MF, (13.2.44)
xo(t) £ uo(t), o=  r, " rÎ R, (13.2.45)
r, " rÎ R, (13.2.45)
где соотношение opt Fr(Xr(t)) Û opt Fr(Yr(t)) Û opt Fr(Zr(t)) показывает двойную эквивалентность (двойную агрегацию) векторного критерия региона (13.2.27), имеющего переменную Xr(t) размерностью Nn*Пo*Or, " rÎ R, агрегированного векторного критерия Fr(Yr(t)), имеющего переменную Yr(t) размерностью 1*Пo*Or, " oÎ O, рассмотренного в модели (13.2.27)-(13.2.31) и агрегированного векторного критерия Fr(Zr(t)), имеющего переменную Zr(t) размерностью 1*Or, т.е. равно количеству отраслей в регионе;
соотношение opt Fr(Zr(t))«opt Fr(Yr(t)) показывает переобозначение переменных Zr(t) в Yr(t) с учетом (13.2.40);
агрегированный векторный критерий Fr(Yr(t)) состоит из двух подмножеств - первое (13.2.41) представлено одной компонентой vÎ Ko, являющейся агрегированным ведущим критерием отрасли и определяет конечный продукт, получаемый каждой отраслью региона, - второе F2r(Yr(t)) - векторный региональный критерий, каждая компонента которого представляет сумму отдельных критериев отраслей, обладающих свойствами аддитивности, и характеризует технико-экономические показатели региона;
(13.2.43) - агрегированные ограничения, связанные с прямыми затратами i-ой отрасли в o-ой " i, oÎ O, они эквивалентны ограничениям (13.2.4) и составлены из (13.2.40); (13.2.44) - ограничения, определяемые трудовыми ресурсами и производственными фондами отраслей, они эквивалентны ограничениям (13.2.5) и составлены суммированием (13.2.37);
для вектора переменных представленного соотношениями (13.2.45) эквивалентным является агрегированный вектор (13.2.31).
Прежде чем приступить к анализу агрегированной модели (13.2.41)-(13.2.45), заметим, что максимизируемый конечный продукт (13.2.41) представляет собой составляющие: yoпотр, o=  - продукция на цели личного и общественного потребления; yoф, o=
- продукция на цели личного и общественного потребления; yoф, o=  - накопление основных и оборотных фондов; yoэ, o=
- накопление основных и оборотных фондов; yoэ, o=  - экспорт; yoост, o=
- экспорт; yoост, o=  - возмещение основных производственных фондов, государственных резервов и т. д. поэтому решая ВЗЛП модели (13.2.41)-(13.2.45) для каждого из перечисленных показателей (критериев), можем получить пределы их роста (0£ yo £ yo*, o=
- возмещение основных производственных фондов, государственных резервов и т. д. поэтому решая ВЗЛП модели (13.2.41)-(13.2.45) для каждого из перечисленных показателей (критериев), можем получить пределы их роста (0£ yo £ yo*, o=  ), и условия, когда критерии равнозначны.
), и условия, когда критерии равнозначны.
В результате решение задачи (13.2.41)-(13.2.45) на планируемый год tÎ T получим: точку оптимума Yro(t)={yoo(t), o=  r} и максимальную относительную оценку lo(t), такую, что
r} и максимальную относительную оценку lo(t), такую, что
lo(t)=lo(yoo(t)), o=  r, (13.2.46)
r, (13.2.46)
для критерия (13.2.41), т. к. критерии (отрасли) независимы, и
lo(t) £ lk (yoo(t)), k=  r, (13.2.47)
r, (13.2.47)
для критерия (13.2.42), т.е. lo(t) является максимальным нижним уровнем для всех относительных оценок lk(X(t)), k=  или гарантированным результатом в относительных единицах, а в соответствии с теоремой 3, точка {Yo, lo } оптимальна по Парето.
или гарантированным результатом в относительных единицах, а в соответствии с теоремой 3, точка {Yo, lo } оптимальна по Парето.
Полученная точка оптимума Yoo(t)={yno(t), п=  o} определяет агрегированный конечный вид продукции, выпускаемый каждой отраслью, технико-экономические показатели региона, включенные в план, и соответствующие межотраслевые затраты xij(t)=
o} определяет агрегированный конечный вид продукции, выпускаемый каждой отраслью, технико-экономические показатели региона, включенные в план, и соответствующие межотраслевые затраты xij(t)=  aij xi(t), " iÎ O.
aij xi(t), " iÎ O.
Подставляя значения yoo(t), " oÎ Or в критерии (13.2.41) и ограничения (13.2.43) в отраслевом разрезе получим информационную модель отрасли на планируемый год tÎ T:
Imo(t)={ yoo(t), fk(yoo(t))=  cok yoo(t), k=
cok yoo(t), k=  r, Kr=
r, Kr= 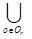 Ko,
Ko,
Gi(yoo(t)), i= 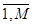 o, o=
o, o=  , i=
, i= 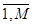 tr, i=
tr, i= 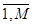 f}, " oÎ O. (13.2.48)
f}, " oÎ O. (13.2.48)
Полученная модель эквивалентна ИМ (13.2.26), но в качестве переменной здесь используется конечный продукт отрасли.
Объединяя все ИМ отраслей на планируемый год tÎ T получим агрегированную ИМ региона:
Imr(t)={ Yro(t)={yoo(t), o=  r}, fk(Yro(t))=
r}, fk(Yro(t))=  cok yoo(t), k=
cok yoo(t), k=  o,
o,
Gi(Yoo(t)), i= 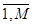 o, o=
o, o=  , i=
, i= 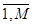 tr, i=
tr, i= 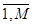 f}, " rÎ R. (13.2.49)
f}, " rÎ R. (13.2.49)
Полученные ИМ могут быть использованы в модели следующего уровня государство-регион.
При решении ВЗЛП (13.2.41)- (13.2.45) на период tÎ T лет получим развитие региона в динамике в виде набора ИМ на каждый период планирования.