Моделирование региональной экономики в динамике

Математическая модель развития экономики региона (14.1.10)-(14.1.16) с учетом воспроизводства предполагает при каждом просчете изменение показателей на планируемый период tÎ T. Для создания автоматизированной технологии расчета на несколько лет необходимо выявить те показатели (факторы), которые ежегодно изменяются при развитии экономики региона. К ним относятся:

трудовые ресурсы, зависящие от демографии региона, минимальное значение (отчетное за текущий год) Tzmin(t⁰+∆ t)=temp* Tzmin(t⁰+∆ t), где temp темп прироста (убытия) трудовых ресурсов, аналогично Tzmax(t⁰+∆ t)=temp* Tzmax(t⁰) ресурсы на конец планируемого периода, - это находит отражение в неравенстве (14.2.5¢);

рост производственных мощностей за планируемый период Xinv(t⁰+∆ t)=KX*Xinv(t⁰), где KX коэффициент прироста производственных мощностей;

рост инвестиций за планируемый период Iinv(t⁰+∆ t)=Kinv*Iinv(t⁰), где Kinv коэффициент прироста инвестиций;

рост конечного использования (спроса) за планируемый период Ymax(t⁰+∆ t)=KY*Ymax(t⁰), где KY коэффициент прироста продукции конечного использования;

Цель развития региональной экономики направлена улучшение благосостояния населения региона, т. е. увеличения (максимизации) продукции конечного использования (спроса - КС) всех видов деятельности региона, с учетом их воспроизводства на каждый период планирования. Эта целенаправленность можно выразить в виде векторной задачи линейного программирования:

Opt F(X, I, Y)= {Y(t) = {max y_j(t), j = }, (14.2.1)

max Y^val(t)= y_j(t), max X^val(t)= x_j(t)}, (14.2.2)

при ограничениях

(I-A)X(t)-V I (t) ³ Y(t), (14.2.3)

X(t)=(1-k^изн)X(t⁰) + φ I (t), (14.2.4)

RX(t) ≤ b(t⁰+∆ t) + ∆ b(t), (14.2.5)

Tzmin≤ R_trudX(t)≤ Tzmax, (14.2.5¢)

Xinv(t⁰) ≤ X(t) ≤ Xinv(t⁰+∆ t), Xinv(t⁰+∆ t)=KX*Xinv(t⁰),

I inv (t⁰) ≤ I (t) ≤ I inv (t⁰+∆ t), I inv(t⁰+∆ t)=Kinv* I inv(t⁰),

Ymax(t⁰)≤ Y(t)≤ Ymax(t⁰+∆ t), Ymax(t⁰+∆ t)=KY*Ymax(t⁰), (14.2.6)

∆ t= t⁰, t⁰+1, …, t⁰+T, (14.2.7)

где (14.2.1)– векторный критерий максимизации КС видов деятельности; (14.2.2) - суммарный (валовой) конечный спрос (использование) и выпуск регионального продукта соответственно; (14.2.3) - межотраслевые балансовые ограничения с учетом инвестиций; (14.2.4) – блок воспроизводства выпуска продукции с учетом инвестиций соответствует (14.1.6):

I (t)=φ _jk_j^ам I _j^ам(t) + φ _j I _j^ин(t), j= ;

(14.2.5) – ограничения по ресурсам; (14.2.6)- ограничения по производственным мощностям, инвестициям и КС отраслей

Xmin(t)={Xinv(t⁰) I inv (t⁰) Ymax(t⁰)},

Xmax(t⁰+∆ t)={KX*Xinv(t⁰) Kinv* I inv(t⁰) KY*Ymax(t⁰)}

на соответствующий планируемый период ∆ t=0, 1, …, T.

Задача (14.2.1)-(14.2.7) представляет векторную задачу линейного программирования являющейся математической моделью развития экономики региона с учетом воспроизводства на планируемый период tÎ T.

Для решения задачи (14.2.1)-(14.2.7) используется алгоритм, основанный на нормализации критериев и принципе гарантированного результата [6].

Задача (14.2.1)-(14.2.7) решается в динамике с периодом планирования, как правило, один год, ∆ t=0, 1, 2, …, T.

В результате решения получим:

1) точку оптимума:

X^o(t) ={X^o(t)={x (t), j= }, I ^o(t)={ I (t), j = }, Y^o(t)={y (t), j = }},

где X^o(t) - валовые выпуски, I ^o(t) - инвестиции для всех отраслей (видов деятельности) и Y^o(t) - конечное использование региона на период планирования tÎ T;

2) конечное использование всех отраслей измеренное в относительных единицах - l_j(y (t)), j = , - такое измерение позволяет сравнивать развитие отраслей друг с другом:

l_j(y (t))= , j = ,

где f 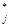- наилучшее решение задачи (14.2.1)-(14.2.7) по j-му критерию (отрасли), f - наихудшее решение задачи (14.2.1)-(14.2.7) по j-му критерию;

3) максимальный относительный уровень l^o(t) для всех критериев l_j(y (t)), j= , он также называется гарантированным результатом в относительных единицах, который гарантирует, что все отрасли, измеренные в относительны единицах, l_j(y (t)) в точке оптимума {X^o(t), I ^o(t), Y^o(t)} равны или больше l^o(t), т.е. l_j(y (t)) ³ l^o(t), или

l^o(t) ≤ l_j(y (t)), j = ;

т. к. критерии (виды деятельности) независимы [6], то l^o(t)=l_j(y 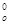(t)), j= , для критерия (14.2.0), и l^o(t) £ l_k(y (t)), k=1, 2 для критериев (14.2.1)-(14.2.2), т. е. l^o(t) является максимальным нижним уровнем для всех относительных оценок l_k(X(t)), k= , а в соответствии с теоремой 2 стр. 29 [6], точка {l^o, X^o, Y^o} оптимальна по Парето;

4) полученная точка оптимума {X^o, Y^o, I ^o(t)} дает возможность определить основные технико-экономические показатели региона, включенные в план, и соответствующие межотраслевые затраты:

x_ij(t)= a_ijx_i(t), " iÎ N.