Стандартные оптимизационные модели региона, учитывающие межотраслевой баланс

Оптимизационные межотраслевые модели региона развивают и усиливают аналитические возможности моделей балансового типа. Во-первых, основные условия балансовых моделей обязательно включаются в оптимизационные модели, и поэтому балансовые модели могут интерпретироваться как частный случай оптимизационных моделей. Во-вторых, оптимизационные модели позволяют упорядочить и формализовать выбор наилучшего из сбалансированных состояний экономики региона с точки зрения определенных критериев оптимальности (целевых функций). В-третьих, решение оптимизационной модели наряду с " оптимальным планом" дает важную информацию о со измерителях затрат и результатов - оптимальные оценки (оптимальные значения двойственных переменных, или " объективно обусловленные оценки"), а также другие показатели, характеризующие изменения " оптимального плана" при изменении различных условий модели [51].

Критерий оптимальности (или целевая функция) региона выражает стремление к максимизации благосостояния населения в рамках условий устойчивого социо-экономико-экологического развития региональной системы. Для краткосрочного периода прогнозирования, как правило, применяются критерии максимизации внутреннего конечного спроса или его основной части - конечного потребления при фиксировании прочих частей конечного спроса. Расчеты по оптимизационной модели могут включать процедуры уточнения критерия оптимальности.

Рассмотрим несколько модификаций критерия оптимальности в межотраслевой модели региона.

1. Максимизация внутреннего конечного спроса (или конечного потребления) в заданном ассортименте, модель которого представим в следующем виде:

z 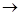max, (12.8.1)

(I - A)X - z Q, (12.8.2)

RX B, (12.8.3)

X_j М_j, j= , (12.8.4)

где z - величина общего объема внутреннего конечного спроса, z={y₁+ y₂}, y₁ - конечное потребление, y₂ - конечное накопление, Q={q_j, j= } вектор-столбец фиксированных величин КС (например, сальдо внешних связей), y=z+Q - конечный спрос; R - матрица ресурсных коэффициентов, B - вектор имеющихся ресурсов в регионе; М = {М_j, j= } - вектор-столбец производственных мощностей по каждой j-ой отрасли; =( _j, j= ) - вектор-столбец структуры внутреннего КС, для удобства принимаем: 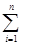_i=1.

Модель в такой форме имеет 2n линейных неравенств и (n + 1) основных переменных. Решение модели существует, если значения компонентов вектора Q заданы не слишком большие.

2. Максимизация прироста внутреннего КС в заданном ассортименте:

z 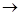max, (12.8.5)

y_i = y_i⁰ + b_i z, i = , (12.8.6)

(I - A)X - Y Q, (12.8.7)

RX B, (12.8.8)

X_j М_j, j= , (12.8.9)

где y_i⁰ - КС i-ой отрасли в базисном году; b={b_{i j}, j= } - вектор-столбец коэффициентов структуры прироста внутреннего КС. Принимаем: 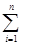b_i = 1; z - величина прироста общего объема КС.

3. Максимизация векторной функции внутреннего КС:

Y 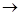max, (12.8.10)

(I - A)X - Y Q, (12.8.11)

RX B, (12.8.12)

X_j М_j, j= . (12.8.13)

Принципиальное отличие векторной максимизации КС от рассмотренных выше скалярны х критериев оптимальности выражается в том, что отраслевая (натуральная) структура КС заранее не выбирается и оптимизация выполняется одновременно по всем отраслям региона. Решение векторной оптимизационной модели региона рассмотрено в следующем разделе.

12.8.2. Построение оптимизационных моделей на примере экономики Приморского края.

1. Максимизация внутреннего конечного спроса (или конечного потребления) в заданном ассортименте - модель (12.8.1)-(12.8.4) [51].

Пример 1. (Модель Приморского края за 1999 год)

Проиллюстрируем оптимизационную модель (12.8.5)-(12.8.9), используя для расчетов исходный межотраслевой баланс, структура которого представлена в [52]. Матрицы затрат и ограничения по ресурсам представим ниже. В составе внутреннего конечного спроса зафиксируем у₁ = 12000 тыс. руб., поскольку нет особого смысла стремиться к увеличению использования сырья сверх нормативных потребностей. Вектор a будет включать положительные компоненты a₂ = 0, 72 и a₃ = 0, 28. Вектор Q будет включать фиксированное сальдо внешних связей и у₁ = 12000, т. е.:

a= , Q = , N = .

Переходим к следующей задаче, соответствующей (2.5.3):

z® max, (12.8.14)

0.927x₁ - 0.253x₂ - 0.150x₃ ³ 30425.2, (12.8.15)

-0.048x₁ + 0.832x₂ - 0.188x₃ –0.78z ³ -6580.4, (12.8.16)

-0.121x₁ - 0.168x₂ + 0.962x₃ –0.28z ³ 5948.3, (12.8.17)

x₁£ 51000, x₂£ 53000, x₃£ 36000, x₁, x₂, x₃, z ³ 0, (12.8.18)

Решаем эту задачу в системе Matlab – версия 6.1. М-файл решения задачи линейного программирования (12.8.14)-(12.8.18) представлен в Приложении 8.

В результате решения получим оптимальные значения переменных:

X^* ={x₁^* = 51000, x₂^* = 45936, x₃^* = 35058, z^* = 49626}.

b = (I - A)^-1 = ; (I - A)^-1Q = ; N₁ = .

Максимальное значение (величина максимизируемого внутреннего конечного спроса) z^* = 49626; Y₃ = 35731, Y₂ = 13895.

Оптимальные значения переменных: x₁^* = 51000, x₂^* = 45936, x₃^* = 35058.

Отметим, что потребность в трудовых ресурсах составляет 933 тыс. чел., что меньше имеющегося ресурса (1000 тыс. чел.).

Двойственная переменная задачи имеет следующее оптимальное значение U₁^* = 2, 81. Увеличение производственной мощности на " малую" единицу позволяет увеличить максимизируемую переменную z^* на 2, 88 единицы.

Рассмотрим теперь модификацию модели с критерием максимизации конечного потребления. В данном случае меняются значения векторов и Q. Вектор теперь будет характеризовать структуру конечного потребления, а вектор Q - дополнительно включать валовое накопление.

В результате решения задачи получим: z^* = 50789, y₂ = 18792, y₃ = 31997. Т. о. Величина максимизируемого конечного потребления равна 50789 тыс. руб. Она лимитируется производственной мощностью отрасли " Добыча". Весь объем конечного потребления, включая зафиксированные 12000 по отрасли " Добыча" составляет 62789 тыс. руб. Сравнивая эту величину с объемом конечного потребления в исходном МОБе, находим выигрыш от оптимизации: 16%. Оптимальные значения переменных: Х₁ = 51000, Х₂ = 34413, 8, Х₃ = 54416, 5.

Теперь предположим, что общим ограниченным ресурсом является труд. Для того, чтобы временно отключить действия ограничений по производственным мощностям, примем N₁ = 51500. В результате этой корректировки лимитирующим ресурсом становится труд, а не производственные мощности. В результате расчетов получим следующие данные: z^* = 54371, x₁^* = 52687, x₂^* = 50690, x₃^* = 37481. По сравнению с предыдущим оптимальным решением на максимум конечного спроса целевой показатель увеличился на 3582, объемы выпусков также увеличились. Оптимальная оценка труда составляет 66, 23; это означает, что при увеличении лимита трудовых ресурсов на единицу величина максимизируемого конечного спроса возрастет на 66, 23.

Пример 2. (Модель Приморского края за 2003 год – вариант 1)

Проиллюстрируем оптимизационную модель (12.8.1)-(12.8.4), используя для расчетов исходный межотраслевой баланс (см. в [52]).

Матрицы затрат и ограничения по ресурсам полностью сохраняется.

В составе внутреннего конечного спроса зафиксируем у₁ = 12000 тыс. руб., поскольку нет особого смысла стремиться к увеличению использования сырья сверх нормативных потребностей. Вектор a будет включать положительные компоненты a₂ = 0, 72 и a₃ = 0, 28. Вектор Q будет включать фиксированное сальдо внешних связей и у₁ = 12000, т. е.:

a= , Q = , N = .

Переходим к следующей задаче, соответствующей (2.5.3):

z® max, (12.8.19)

0.9 x₁ - 0.27 x₂ - 0.16 x₃ ³ 33200, (12.8.20)

-0.05 x₁ + 0.84 x₂ - 0.2 x₃ –0.78z ³ -7600, (12.8.21)

-0.14 x₁ - 0.15 x₂ + 0.93 x₃ –0.28z ³ 11900, (12.8.22)

x₁£ 66000, x₂£ 50000, x₃£ 76000, x₁, x₂, x₃, z ³ 0. (12.8.23)

Решаем эту задачу в системе Matlab – версия 6.1. М-файл решения задачи линейного программирования (12.8.19)-(12.8.23) представлен в Приложении 8.

В результате решения получим оптимальные значения переменных:

X^* ={x₁^* = 59990, x₂^* = 50000, x₃^* = 45567, z^* = 52066}.

Пример 3. (Модель Приморского края за 2003 год – вариант 2)

Проиллюстрируем оптимизационную модель (12.8.19)-(12.8.23), предполагая, что конечный спрос представляет сумму отраслей:

z= y₁ + y₂ + y₃.

В итоге задача примет следующий вид:

(y₁ + y₂ + y₃)® max, (12.8.24)

0.9 x₁ - 0.27 x₂ - 0.16 x₃ - y₁ ³ 0, (12.8.25)

-0.05 x₁ + 0.84 x₂ - 0.2 x₃ - y₂ ³ 0, (12.8.26)

-0.14 x₁ - 0.15 x₂ + 0.93 x₃ - y₃³ 0, (12.8.27)

x₁£ 66000, x₂£ 50000, x₃£ 76000, (12.8.28)

x₁, x₂, x₃, y₁, y₂, y₃ ³ 0,

Решаем эту задачу в системе Matlab – версия 6.1. М-файл решения задачи линейного программирования (12.8.24)-(12.8.28) представлен в Приложении 8.

В результате решения получим оптимальные значения переменных:

X^* ={x₁^*= 66000, x₂^*=50000, x₃^*=76000, y₁^*=33740, y₂^* =23500, y₃^*= 53940},

z^* =y₁+ y₂ + y₃ = 111180.

Сравнивая результаты решения примеров 2 и 3 видим, что во втором случае загрузка отраслей значительно выше и это говорит о потенциальных возможностях оптимизационных методов.

Пример 4. (Модель Приморского края за 2003 год – с критерием максимизации конечного потребления)

Рассмотрим теперь модификацию модели с критерием максимизации конечного потребления.

В данном случае меняются значения векторов a и Q. Вектор a теперь будет характеризовать структуру конечного потребления, а вектор Q - дополнительно включать валовое накопление.

Вектор a будет включать положительные компоненты a₂=0, 72 и a₃=0, 28.:

a= , Q = , N = .

Переходим к следующей задаче, соответствующей (12.8.10)-(12.8.13):

z® max, (12.8.29)

0.9 x₁ - 0.27 x₂ - 0.16 x₃ ³ 33200, (12.8.30)

-0.05 x₁ + 0.84 x₂ - 0.2 x₃ –0.6667z ³ -2700, (12.8.31)

-0.14 x₁ - 0.15 x₂ + 0.93 x₃ –0.3333z ³ 16100, (12.8.32)

x₁£ 66000, x₂£ 50000, x₃£ 76000, x₁, x₂, x₃, z ³ 0, (12.8.33)

Решаем эту задачу в системе Matlab – версия 6.1. М-файл решения задачи линейного программирования (12.8.29)-(12.8.33) представлен в приложении 7.

В результате решения получим оптимальные значения переменных:

X^* ={x₁^* = 61031, x₂^* = 50000, x₃^* = 51423, z^* = 47043}.

Пример 5. (Модель векторной оптимизации)

В задачах векторной оптимизации имеется множество целей (критериев), по которым выполняется совместная оптимизация. В качестве алгоритма решения в [1] предложен метод аддитивного критерия, а в этой работе для решения векторной задачи математического программирования развивается метод, основанный на нормализации критериев и принципе гарантированного результата.

Критериями являются конечный спрос агрегированных отраслей, которые в совокупности представляют векторный критерий: Y={y_j, j= }.

Ограничениями являются, во-первых, межотраслевой баланс, во-вторых, ресурсные ограничения и ограничения по производственным мощностям.

С учетом сказанного, векторная задача, моделирующая развитие экономики региона на планируемый период, примет вид:

opt Y = {max y_j, j= }, (12.8.34)

(I - A)X - Y 0, (12.8.35)

RХ B, (12.8.36)

0 X M, (12.8.37)

Y 0, (12.8.38)

где (12.8.34) – представляет векторный критерий максимизации конечного спроса, (12.8.35) – межотраслевые балансовые ограничения, (3.6.3)– ограничения по ресурсам, (12.8.36) – ограничения по мощностям отраслей, (12.8.37) – не отрицательность конечного спроса отраслей.

Для Приморского края эта модель, предполагая, что общим ограниченным ресурсом является труд, примет вид:

opt Y = {max y₁, max y₂, max y₃}, (12.8.39)

0.9 x₁ - 0.27 x₂ - 0.16 x₃ - y₁ ³ 0, (12.8.40)

-0.05 x₁ + 0.84 x₂ - 0.2 x₃ - y₂ ³ 0, (12.8.41)

-0.14 x₁ - 0.15 x₂ + 0.93 x₃ - y₃³ 0, (12.8.42)

0, 0032x₁ + 0, 0107x₂ + 0, 010x₃ £ 1.4, (12.8.43)

x₁£ 66000, x₂£ 50000, x₃£ 76000, (12.8.44)

x₁, x₂, x₃, y₁, y₂, y₃ ³ 0,

Решаем эту задачу в системе Matlab – версия 6.1. М-файл решения задачи линейного программирования (12.8.39)-(12.8.44) представлен в Приложении 8.

Результаты решения векторной задачи представим в виде последовательности шагов.

Шаг 1. Решаем задачу (12.8.39)-(12.8.44) по каждому критерию отдельно.

Результаты решения по первому критерию: f = 55874.

X ={x₁^*= 66000, x₂^*= 6546, x₃^*=10991, y₁^*=55874, y₂^* =0.0, y₃^*= 0.0},

Результаты решения по второму критерию: f 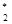= 39034.

X 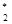={x₁^*= 16886, x₂^*= 5.0000, x₃^*=1.0606, y₁^*=0.0, y₂^* =3.9034, y₃^*= 0.0},

Результаты решения по третьему критерию: f = 65094.

X ={x₁^*= 19284, x₂^*= 19243, x₃^*=7.6000, y₁^*=0.0, y₂^* =0.0, y₃^*= 6.5094},

Шаг 2. Строится l-задача.(Заметим, f^o=0)

max l,

l - y₁/f £ 0, (12.8.45)

l - y₂/f 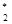£ 0, (12.8.46)

l - y₃/f £ 0, (12.8.47)

0.9 x₁ - 0.27 x₂ - 0.16 x₃ - y₁ ³ 0, (12.8.48)

-0.05 x₁ + 0.84 x₂ - 0.2 x₃ - y₂ ³ 0, (12.8.49)

-0.14 x₁ - 0.15 x₂ + 0.93 x₃ - y₃³ 0, (12.8.50)

0, 0032x₁ + 0, 0107x₂ + 0, 010x₃ £ 1.4, (12.8.51)

x₁£ 66000, x₂£ 50000, x₃£ 76000, (12.8.52)

x₁, x₂, x₃, y₁, y₂, y₃ ³ 0, (12.8.53)

Шаг 3. Решается l-задача (12.8.47)-(12.8.53).

В результате решения получим оптимальные значения переменных:

X^o ={x₁^o= 36098, x₂^o= 26777, x₃^o=34483, y₁^o=19741, y₂^o =13791, y₃^o= 22999},

l^o = 0.3533.

l₁(X^o)=f₁(X^o)/f =19741/55874= 0.3533.

l₂(X^o)=f₃(X^o)/f =13791/39034= 0.3533.

l₃(X^o)=f₃(X^o)/f = 22999/65094= 0.3533.

Таким образом, все критерии (отрасли – конечный спрос) подняты до максимально возможного уровня. Любое улучшение одного из критериев приводит к ухудшению других критериев (отрасли), т.е. решение оптимально по Парето.