Числовая модель региональной экономики. Основные этапы.

Для разработки числовой модели региональной экономики (14.2.1)-(14.2.7) возьмем значения межотраслевого баланса с отчетными (статистическими) данными за 2004 год [72], представленными в табл. 14.1.

Таблица 14.1

Межотраслевой баланс экономики Приморского края за 2004 г., мл. руб.

Выпуск   Затраты

Промежуточное потребление

Конечное использование

Всего Xi, i=

Промышлен.

С/х

Строительство

Лесн. хоз-во

Услуги

Транспорт

Итого AX

Конеч. Потребление

Вал. накопление

Тов. запасы

Экспорт

Итого Y

Промышлен.

С/х

Строительство

Лес. хоз-во

Услуги

Транспорт

Итого

Опл.труда–Z1

Налоги–Z2

Амортизац.–Z3

Прибыль–Z4

ВДС – Z

Всего ресурс. Xj, j=

Занято, тыс.ч.

61, 1

3, 6

83, 2

534, 7

974, 6

Оценим коэффициенты валовой добавленной стоимости (ВДС) – Z, промежуточного потребления – AX, конечного использования – Y, инвестиций - I.

Валовая добавленная стоимость.

Z1=[26428 3207 3813 822 35899 17582 87751;

3407 1207 1061 210 4208 2328 12421;

6732 10 10 33 13766 7690 28241;

4633 73 89 59 3152 2656 10662;

41200 4497 4973 1124 57025 30256 139075];

Проверка валовойдобавленной стоимости по вертикали и горизонтали.

sumZ1=Z1(:, 1)+Z1(:, 2)+Z1(:, 3)+Z1(:, 4)+Z1(:, 5)+Z1(:, 6)

%SumZ1 = 87751 12421 28232 10671 139075 Проверка Z

sumZ=Z1(1,:)+Z1(2,:)+Z1(3,:)+Z1(4,:)

%SumZ = 41200 4497 4973 1124 57025 30256 139075

Промежуточное потребление и конечное использование.

Balans=[25230 6735 8610 551 8783 3479 53388 19635 3467 8612 3878 35592 88980;

663 648 360 561 693 595 3520 9135 725 1897 0 11757 15277;

1254 965 1120 643 804 821 5607 11645 3862 6235 686 22428 28035;

47 58 49 33 17 16 220 4931 538 189 1458 7116 7336;

15559 1335 5602 2741 4102 6112 35451 25861 924 5120 5002 36907 72358;

5027 1039 7321 1683 934 857 16861 9362 6537 4843 4533 25275 42136].

На основе межотраслевого баланса (Balans и Z1) рассчитаем матрицу прямых затрат A={a_ij, i, j= }, матрицу ВДС – Z={z_ij, i= , j= }, в которых коэффициенты прямых затрат и ВДС определяются следующим образом:

a_ij= ³ 0, i, j= ; z_ij= 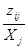³ 0, i= , j= ;

где X_j - объем производства j-ой отрасли; a_ij– коэффициент пропорциональности – определяет прямые затраты; z_ij– коэффициент ВДС.

В итоге получим матрицу коэффициентов прямых затрат:

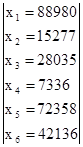А= , X= , Y= .

Zvds =[0.2970 0.2099 0.1360 0.1121 0.4961 0.4173

0.0383 0.0790 0.0378 0.0286 0.0582 0.0552

0.0757 0.0007 0.0004 0.0045 0.1902 0.1825

0.0521 0.0048 0.0032 0.0080 0.0436 0.0630]

Блок ресурсов включает ограничения по трудовым затратам. Коэффициенты трудовых затрат рассчитываются по отдельным отраслям:

T _j^з= 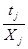, j= ,

где t_j= 1000*[200 92 61.1 3.6 83.2 534.7] берется из баланса (строка - Занято, тыс.ч.). T ^з =[2.2477 6.0221 2.1794 0.4907 1.1498 12.6899].

Блок мощностей включает ограничения по объемам произведенной продукции (отчет) за текущий и плановый период

X^от(j)≤ Х_j≤ X^план(j), j= , где

X^от ={88980 15277 28035 7336 72358 42136}, из табл. 1, а

X^план =X^от +10%X^от»{97878 17000 31000 8500 79000 46000}

Блок инвестиций.

Представим матрицу норм воспроизводства всех видов деятельности V ={j_j={j_ij, i= }, j= }, где j_ij – норма, определяющая долю от величины капиталовложений – j_j по видам деятельности (отраслям), =1, j= , n=6, т.е. j_j= , " jÎ n:

V= . (14.3.1)

Примем коэффициенты: величину износа основных фондов и использования амортизационных отчислений 10%, k^изн=0.1, k^ао=0.1.

Объем инвестиций I _j^ин направлен на восстановление изношенных фондов и создания новых:

Х_j ≤ (1-k^изн+k^ао)X^от+j_j I _j^ин, j= , (14.3.2)

где величина j_j I _j^ин – увеличение объема производства j-ого вида деятельности на величину инвестиций I _j^ин умноженную на коэффициент «фондоотдачи» j_j.

Из неравенства вытекает, что объем инвестиций I _j^ин лежит в пределах от минимального восстановления изношенных основных фондов k^изнX^от/j_j, увеличенных на величину выделенных инвестиций I _j^выд= I _j^ин.ф.+ I _j^ин.рег.+ I _j^ин.гос.:

j^изнX^от/j_j ≤ I _j ≤ k^изнX^от/j_j +j_j I _j^выд, j=

Объем выделенных инвестиций (от фирм, региона, государства) примем I (t⁰+∆ t)= 0.2*X^от, в итоге объем инвестиций по каждой отрасли:

I (t⁰+∆ t)=[ I ₁^ин=17796, I ₂^ин=3055, I ₃^ин=5607, I ₄^ин=1467, I ₅^ин=14472, I ₆^ин=8427].

Коэффициент «фондоотдачи» - использования основных фондов - равен отношению валового объема j-го вида продукции выпушенной t⁰ году в регионе к объему основных фондов φ _j(t⁰)= X_j^val(t⁰)/ Φ _j(t⁰), j= , примем для всех видов продукции φ _j(t⁰)=0.2778.

Используя матрицу А, преобразовав ее к виду (I-A), и матрицу воспроизводства всех видов деятельности V (14.3.1), построим балансовые уравнения задачи вида (14.2.3). В качестве блока ресурсных затрат возьмем трудовые ресурсы (14.2.5¢). Добавим матрицу инвестиций I _j^ин, направленную на восстановление изношенных фондов и создания новых (14.3.2). В итоге, с учетом целенаправленности региона (14.2.1)-(14.2.7), числовая модель экономики региона (Приморского края) в виде векторной задачи линейного программирования примет вид:

Числовая модель экономики Приморского края в виде векторной задачи линейного программирования

Opt Y = {max Y(t⁰+∆ t) = {max y_j(t⁰+∆ t), j = }, Y^val(t⁰+∆ t)= y_j(t⁰+∆ t), X^val(t⁰+∆ t)= x_j(t⁰+∆ t)}, (30)

0.7165 х₁-0.441 х₂ -0.3071х₃-0.0751х₄-0.1214х₅-0.0826х₆ -0.3 I ₁-0.3 I ₂-0.4 I ₃-0.4 I ₄-0.2 I ₅-0.2 I ₆ - у₁≥ 0, (31)

-0.0075х₁+0.9576х₂+0.0128х₃-0.0765х₄-0.0096х₅-0.0141х₆ -0.05 I ₁-0.2 I ₂-0.05 I ₃-0.05 I ₄-0.3 I ₅-0.2 I ₆ -у₂≥ 0,

-0.0141х₁-0.0632х₂+0.9600х₃-0.0876х₄-0.0111х₅-0.0195х₆ -0.3 I ₁-0.3 I ₂-0.3 I ₃-0.2 I ₄-0.2 I ₅-0.2 I ₆ -у₃≥ 0,

-0.0005х₁-0.0038х₂-0.0017х₃+0.9955х₄-0.0002х₅-0.0004х₆ -0.05 I ₁-0.05 I ₂-0.05 I ₃-0.1 I ₄-0.05 I ₅-0.05 I ₆-у₄≥ 0,

-0.1749х₁-0.0874х₂-0.1998х₃-0.3736х₄+0.9433х₅-0.1451х₆ -0.2 I ₁-0.1 I ₂-0.1 I ₃- 0.05 I ₄-0.2 I ₅-0.1 I ₆ -у₅≥ 0,

-0.0565х₁-0.0680х₂-0.2611х₃-0.2294х₄- 0.0129х₅+0.9797х₆-0.1 I ₁-005 I ₂-0.1 I ₃- 0.2 I ₄-0.05 I ₅-0.15 I ₆ - у₆≥ 0, (32)

974.6 ≤ 0.22х₁+0.0066х₂+0.0021х₃+0.0004х₄+0.0012х₅+0.0175х₆ ≤ 1072, (33)

х₁ - 0.2778 I ₁≥ 17796, х₂ - 0.2778 I ₂ ≥ 3055, х₃ - 0.2778 I ₃ ≥ 5607,

х₄ - 0.2778 I ₄ ≥ 1467, х₅ - 0.2778 I ₅ ≥ 14472, х₆ -0.2778 I ₆ ≥ 84270, (34)

88980≤ х₁≤ 97878, 15277≤ х₂ ≤ 17000, 28035≤ х₃ ≤ 31000, 7336≤ х₄ ≤ 8500, 72358≤ х₅≤ 79000, 42136≤ х₆≤ 46000, (35)

0≥ I ₁≥ 17796, 0≥ I ₂≥ 3055, 0≥ I ₃≥ 5607, 0≥ I ₄≥ 1467, 0≥ I ₅≥ 14472, 0≥ I ₆ ≥ 84270, (36)

35592≤ y₁≤ 39150, 11757≤ y₂≤ 12933, 22428≤ y₃≤ 24671, 7116≤ y₄≤ 7827, 36907≤ y₅≤ 40598, 25275≤ y₆≤ 27803. (37)

Xinv(t⁰+∆ t)=KX*Xinv(t⁰), I inv(t⁰+∆ t)=Kinv* I inv(t⁰), Ymax(t⁰+∆ t)=KY*Ymax(t⁰), (38)

∆ t= t⁰, t⁰+1, …, t⁰+T, (39)

где векторный критерий (30) соответствует критериям (20)-(22);

ограничения МОБ (31)-(32) соответствуют (23);

(33) определяют ограничения по трудовым ресурсам региона (25¢);

ограничения по инвестициям (34) определяют воспроизводство основных фондов;

ограничения по мощностям (35) представляют Xinv(t⁰) ≤ X(t) ≤ Xinv(t⁰+∆ t), Xinv(t⁰) - отчетные данные за 2004 год;

Xinv(t⁰+∆ t) – предполагаемые мощности на период (t⁰+∆ t)Î T - на 2005 год;

ограничения по инвестициям (36) представляют I inv (t⁰) ≤ I (t) ≤ I inv (t⁰+∆ t);

ограничения по конечному спросу (37) - Ymax(t⁰)≤ Y(t)≤ Ymax(t⁰+∆ t);

равенства (39) определяют коэффициенты воспроизводства: по мощностям, инвестициям и конечному спросу.

Задача (30)-(39) решается в динамике с периодом планирования один год, ∆ t=0, 1, 2, …, T.

Таким образом, модель экономики региона представлена в вид векторной задачи линейного программирования, учитывающая основные ограничения и динамику развития.

5. Методология моделирования развития региональной экономики

Для решения рассматриваемой задачи (30)-(39) используется алгоритм, основанный на нормализации критериев и принципе гарантированного результата.

Представим исходные данные задачи (30)-(39) в системе Matlab:

критерии:

F = [0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0 0; % max y1

0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0 0; % max y2

0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0 0; % max y3

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0; % max y4

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 0; % max y5

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1; % max y6

-1 -1 -1 -1 -1 -1 0 0 0 0 0 0 0 0 0 0 0 0;

0 0 0 0 0 0 0 0 0 0 0 0 -1 -1 -1 -1 -1 -1];

ограничения: межотраслевого баланса, по трудовым ресурсам и инвестиционные приобретают в системе Matlab следующий вид:

A=[-0.7165 0.4409 0.3071 0.0751 0.1214 0.0826 -0.3 -0.3 -0.4 -0.4 -0.2 -0.2 1 0 0 0 0 0;

0.0075 -0.9576 0.0128 0.0765 0.0096 0.0141 -0.05 -0.2 -0.05 -0.05 -0.3 -0.2 0 1 0 0 0 0;

0.0141 0.0632 -0.9600 0.0876 0.0111 0.0195 -0.3 -0.3 -0.3 -0.2 -0.2 -0.2 0 0 1 0 0 0; 0.0005 0.0038 0.0017 -0.9955 0.0002 0.0004 -0.05 -0.05 -0.05 -0.1 -0.05 -0.05 0 0 0 1 0 0;

0.1749 0.0874 0.1998 0.3736 -0.9433 0.1451 -0.2 -0.1 -0.1 -0.05 -0.2 -0.1 0 0 0 0 1 0;

0.0565 0.0680 0.2611 0.2294 0.0129 -0.9797 -0.1 -0.05 -0.1 -0.2 -0.05 -0.15 0 0 0 0 0 1;

-2.2477 -6.022 -2.1794 -0.4907 -1.1498 -12.69 0 0 0 0 0 0 0 0 0 0 0 0;

2.2477 6.0221 2.1794 0.4907 1.1498 12.69 0 0 0 0 0 0 0 0 0 0 0 0;

-1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0 0 0 0;

0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0 0 0;

0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0 0;

0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0;

0 0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0;

0 0 0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0]

вектор ограничений межотраслевого баланса b_i=0, i = и ограничения по трудовым ресурсам b_i, i =n+1, n+2, где n+1 – ограничения снизу, n+2 – ограничения сверху, b_i, i =n+3, …, n+8, – ограничения по инвестициям:

b=[0 0 0 0 0 0 -974600 1071840 (1-Kizn+Kao)*Xot(1) (1-Kizn+Kao)*Xot(2) (1-Kizn+Kao)*Xot(3) (1-Kizn+Kao)*Xot(4) (1-Kizn+Kao)*Xot(5) (1-Kizn+Kao)*Xot(6)]

Aeq=[]; beq=[];

Xmin = [Xot Imin Yot]

Xmin = [Xot=(88980 15277 28035 7336 72358 42136) Imin=(0 0 0 0 0 0) Yot=(35592 11757 22428 7116 36907 25275)] - нижняя граница;

Xmax=[(Xinv=(97878 17000 31000 8500 79000 46000) Iinv=(17796 3055 5607 1467 14472 8427) Ymax=(39150 12933 24671 7827 40598 27803)] - верхняя граница на валовые объемы регионального продукта, инвестиций и конечного спроса по отдельным отраслям x_j, I _j, y_j, j = .

Введем коэффициенты, определяющие развитие: объемов валового регионального продукта KX=1; инвестиций Kinv=0.05; конечного спроса KY=1;

Xmax = [KX*Xinv Kinv*Iinv KY*Ymax]

bl=Xmin; bu=Xmax.

Алгоритм решения представим в виде последовательности шагов, структура которых представлена в [6, 16].

Шаг 1. Решается задача по каждому критерию отдельно. Для этого определяется наихудшие {x1min – x8min} и наилучшие точки оптимума {x1max – x8max} с соответствующими величинами целевых функций: {f1min – f8min} и {f1max – f8max}.

1 критерий: [x1min, f1min] = linprog(-1*F(1,:), A, b, Aeq, beq, bl, bu);

[x1max, f1max] = linprog(F(1,:), A, b, Aeq, beq, bl, bu);

Результаты решения - точки оптимума по первому критерию (отрасли) объединены в вектор X1MinMax =[x1min x1max]', который представим в виде таблицы:

[x1min =9.2076 1.6765 2.9665 0.8010 7.5040 4.4406 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 3.5592 1.2366 2.3032 0.7383 3.7316 2.5905

x1max =9.5779 1.6603 2.9303 0.7981 7.5080 4.4097 0.0631 0.0089 0.0173

0.0039 0.0481 0.0259 3.9150 1.2369 2.3047 0.7393 3.7259 2.5801].

Zagol = Summa X Summa Inv Summa Y

Сумма инвестиций

SuX_Inv_Y = 1.0e+005 * 2.6596 0.0000 1.4159

2.6884 0.0167 1.4502

F1MinMax =[f1min f1max]=[35592 -39150]. d1=-f1max-f1min = 3558

Подсчитывается загрузка ресурсов (трудовых):

r1=-A(7,:)*x1min; dr1=b(7)-r1; r2=A(8,:)*x1max; dr2=b(8)-r2;

Zagol = TrudRes.Othet Dr1=bmin-r1 TrudRes.Plan Dr2=bmax-r2

Res_zan1 = 1026300 -51700 1029000 42900

2 критерий: [x2min, f2min] = linprog(-1*F(2,:), A, b, Aeq, beq, bl, bu);

[x2max, f2max] = linprog(F(2,:), A, b, Aeq, beq, bl, bu);

Результаты решения: X2MinMax =

[X2Min= 9.2220 1.6675 2.9663 0.8023 7.5001 4.4410 0.0000 0.0000

0.0000 0.0000 0.0000 3.5885 1.1757 2.3036 0.7386 3.7270 2.5904

X2Max= 9.1166 1.6893 2.9438 0.7914 7.4073 4.4301 0.0607 0.0104 0.0179

0.0060 0.0494 0.0269 3.5811 1.2933 2.3158 0.7404 3.7175 2.6009].

SuInv = 1.0e+003 * 0.0000 1.7122

F2MinMax = [11757 -12933]; d2 = 1176;

Res_zan2 = 1026100 -51500 1022000 49800.

3 критерий: [x3min, f3min] = linprog(-1*F(3,:), A, b, Aeq, beq, bl, bu);

[x3max, f3max] = linprog(F(3,:), A, b, Aeq, beq, bl, bu);

Результаты решения: X3MinMax =

[x3min=9.2266 1.6768 2.9421 0.8015 7.5001 4.4405 0.0000 0.0000 0.0000

0.0000 0.0000 0.0000 3.5911 1.2369 2.2428 0.7385 3.7312 2.5926

x3max =9.2032 1.6703 3.0489 0.7974 7.4946 4.4374 0.0650 0.0094 0.0179

0.0044 0.0493 0.0267 3.5920 1.2407 2.4671 0.7393 3.7330 2.5873],

F3MinMax =[22428 -24671]; d3 = 2243

Res_zan3 = 1026100 -51500 1027100 44800.

4 критерий: [x4min, f4min] = linprog(-1*F(4,:), A, b, Aeq, beq, bl, bu);

[x4max, f4max] = linprog(F(4,:), A, b, Aeq, beq, bl, bu).

Результаты решения: X4MinMax=

[x4min =9.2336 1.6758 2.9650 0.7936 7.5030 4.4387 0.0000 0.0000 0.0000

0.0000 0.0000 0.0000 3.5905 1.2365 2.3028 0.7116 3.7310 2.5900

x4max =9.1663 1.6762 2.9565 0.8215 7.4699 4.4363 0.0584 0.0092 0.0168

0.0048 0.0460 0.0253 3.5916 1.2428 2.3146 0.7827 3.7317 2.5953].

F4MinMax = [7116 -7827]; d4 = 711;

Res_zan4 = 1026400 -51800 1026600 45300.

5 критерий: [x5min, f5min] = linprog(-1*F(5,:), A, b, Aeq, beq, bl, bu);

[x5max, f5max] = linprog(F(5,:), A, b, Aeq, beq, bl, bu).

Результаты решения: X5MinMax =

[x5min =9.2316 1.6763 2.9662 0.8010 7.4751 4.4405 0.0000 0.0000 0.0000

0.0000 0.0000 0.0000 3.5907 1.2367 2.3031 0.7384 3.6907 2.5902

x5max =9.2173 1.6638 2.9505 0.8020 7.8040 4.4239 0.0590 0.0080 0.0160

0.0029 0.0463 0.0246 3.5937 1.2323 2.3092 0.7389 4.0598 2.5882].

F5MinMax = [36907 -40598]; d5 = 3691;

Res_zan5 = 1026700 -52100 1026300 45600.

6 критерий: [x6min, f6min] = linprog(-1*F(6,:), A, b, Aeq, beq, bl, bu);

[x6max, f6max] = linprog(F(6,:), A, b, Aeq, beq, bl, bu)

Результаты решения: X6MinMax =

[x6min =9.1339 1.6614 2.9097 0.7906 7.4632 4.5478 0.0632 0.0092 0.0174

0.0000 0.0000 0.0000 3.5915 1.2368 2.3052 0.7386 3.7313 2.5275

x6max =9.1339 1.6614 2.9097 0.7906 7.4632 4.5478 0.0632 0.0092 0.0174

0.0045 0.0481 0.0272 3.5886 1.2397 2.2991 0.7381 3.7318 2.7803].

F6MinMax = [25275 -27803]; d6 = 2528;

Res_zan6 =[1022800 -1997400 1038600 33300];

F6MinMax = [25275 -27803]; d6 = 2528;

Res_zan6 = 1022800 -1997400 1038600 33300.

7 критерий: [x7min, f7min] = linprog(-1*F(7,:), A, b, Aeq, beq, bl, bu);

[x7max, f7max] = linprog(F(7,:), A, b, Aeq, beq, bl, bu)

Результаты решения: X7MinMax =

[x7min= 8.8980 1.5277 2.8035 0.7336 7.2361 4.2136 0.0000 0.0001 0.0000

0.0000 0.0012 0.0000 3.5594 1.1757 2.2428 0.7119 3.6907 2.5277

x7max =9.7878 1.7000 3.1000 0.8500 7.9000 4.6000 0.0473 0.0077 0.0145

0.0033 0.0392 0.0222 3.6637 1.2339 2.3367 0.7442 3.7593 2.5940].

SuInv = 1.0e+004 * 0.0127 1.3404

f7min_max = [254120 -279380]; d7 = 25256;

Res_zan7 = 974600 0 1068700 3200.

8 критерий: [x8min, f8min] = linprog(-1*F(8,:), A, b, Aeq, beq, bl, bu);

[x8max, f8max] = linprog(F(8,:), A, b, Aeq, beq, bl, bu)

Результаты решения: X8MinMax =

[91867 16730 29624 8059 74632 44116 35592 11757 2.2428 7116 36907 25275

97721 16796 30824 8063 79000 46000 39150 12933 24671 7827 40116 27486];

SuInv = 14192 22250

f8min_max = [139080 -1529800]; d8 = 13907;

Res_zan8 = 1025000 -50400 1035600 36300.

Экономический смысл первого шага заключается в том, что каждой отрасли последовательно предоставляются все ресурсы и все мощности региона. Данные решения отображают значения конечного спроса, полученные путем вложения всех имеющихся средств у региона в развитие одной отрасли (каждой отрасли). Эти максимальные показатели развития каждой отрасли используем как цели развития этих отраслей.

d = 3558 1176 2243 711 3691 2528 25252 13907

Шаг 2. Построение λ – задачи - (Числовая модель экономики региона - Приморского края) – в ней требуется определить:

λ ^o=max λ, (40)

λ – (y₁- f₁⁰) /d₁ ≤ 0, λ – (y₂- f₂⁰) /d₂ ≤ 0, λ – (y₃- f₃⁰) /d₃ ≤ 0,

λ – (y₄- f₄⁰) /d₄ ≤ 0, λ – (y₅- f₅⁰) /d₅ ≤ 0, λ – (y₆- f₆⁰) /d₆ ≤ 0, (41)

0+0.716х₁-0.441х₂-0.307х₃-0.075х₄-0.121х₅-0.0826х₆-0.3 I ₁-0.3 I ₂-0.4 I ₃-0.4 I ₄-0.2 I ₅-0.2 I ₆ -у₁≥ 0, (42)

0-0.0075х₁+0.9576х₂+0.0128х₃-0.0765х₄-0.0096х₅-0.014х₆-0.05 I ₁-0.2 I ₂-0.05 I ₃-0.05 I ₄-0.3 I ₅-0.2 I ₆-у₂≥ 0,

0-0.0141х₁-0.0632х₂+0.9600х₃-0.0876х₄-0.0111х₅-0.0195х₆-0.3 I ₁-0.3 I ₂-0.3 I ₃-0.2 I ₄-0.2 I ₅-0.2 I ₆ - у₃≥ 0,

0 - 0.0005х₁-0.0038х₂-0.0017х₃+0.9955х₄-0.0002х₅-0.0004х₆ -0.05 I ₁-0.05 I ₂-0.05 I ₃-0.1 I ₄-0.05 I ₅-0.05 I ₆- у₄≥ 0,

0 - 0.1749х₁-0.0874х₂-0.1998х₃-0.3736х₄+0.9433х₅-0.1451х₆ -0.2 I ₁-0.1 I ₂-0.1 I ₃- 0.05 I ₄-0.2 I ₅-0.1 I ₆ - у₅≥ 0,

0 - 0.0565х₁-0.0680х₂-0.2611х₃-0.2294х₄- 0.0129х₅+0.9797х₆-0.1 I ₁-005 I ₂-0.1 I ₃- 0.2 I ₄-0.05 I ₅-0.15 I ₆ - у₆≥ 0, (43)

974.6 ≤ 0+ 0.22х₁+0.0066х₂+0.0021х₃+0.0004х₄+0.0012х₅+0.0175х₆ ≤ 1072, (44)

х₁ - 0.2778 I ₁≥ 17796, х₂ - 0.2778 I ₂ ≥ 3055, х₃ - 0.2778 I ₃ ≥ 5607,

х₄ - 0.2778 I ₄ ≥ 1467, х₅ - 0.2778 I ₅ ≥ 14472, х₆ -0.2778 I ₆ ≥ 84270, (45)

88980≤ х₁≤ 97878, 15277≤ х₂ ≤ 17000, 28035≤ х₃ ≤ 31000,

7336≤ х₄ ≤ 8500, 72358≤ х₅≤ 79000, 42136≤ х₆≤ 46000, (46)

0≥ I ₁≥ 17796, 0≥ I ₂≥ 3055, 0≥ I ₃≥ 5607,

0≥ I ₄≥ 1467, 0≥ I ₅≥ 14472, 0≥ I ₆ ≥ 84270, (47)

35592≤ y₁≤ 39150, 11757≤ y₂≤ 12933, 22428≤ y₃≤ 24671,

7116≤ y₄≤ 7827, 36907≤ y₅≤ 40598, 25275≤ y₆≤ 27803. (48)

Xinv(t⁰+∆ t)=KX*Xinv(t⁰), I inv(t⁰+∆ t)=Kinv* I inv(t⁰), Ymax(t⁰+∆ t)=KY*Ymax(t⁰), (49)

t⁰+∆ t= t⁰, t⁰+1, …, t⁰+T, (50)

Коэффициент λ – это максимальная относительная оценка или гарантированный уровень. Он показывает, до какого уровня подняты все критерии, измеренные в относительных единицах.

Шаг 3. Решение λ – задачи.

λ – задача решается в системе Matlab, для чего строятся исходные данные - критерий и:

Для решения задачи (40)-(50) в системе Matlab представим исходные данные:

критерий L=[-1 0 0 0 0 0 0 0 0 0 0 0 0];

ограничения представлены матрицей

A0 и вектором b0:

A0=[1 0 0 0 0 0 0 0 0 0 0 0 0 -1/d1 0 0 0 0 0;

1 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/d2 0 0 0 0;

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/d3 0 0 0;

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/d4 0 0;

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/d5 0;

1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1/d6;

0 -0.716 0.441 0.307 0.075 0.121 0.082 -0.3 -0.3 -0.4 -0.4 -0.2 -0.2 1 0 0 0 0

0 0.0075 -0.957 0.0128 0.076 0.0096 0.014 -0.05 -0.2 -0.05 -0.05 -0.3 -0.2 0 1 0 0 0 0;

0 0.014 0.0632 -0.96 0.0876 0.011 0.0195 -0.3 -0.3 -0.3 -0.2 -0.2 -0.2 0 0 1 0 0 0;

0 0.0005 0.0038 0.0017 -0.99 0.0002 0.0004 -0.05 -0.05 -0.05 -0.1 -0.05 -0.05 0 0 0 1 0 0;

0 0.1749 0.087 0.1998 0.3736 -0.943 0.1451 -0.2 -0.1 -0.1 -0.05 -0.2 -0.1 0 0 0 0 1 0;

0 0.0565 0.068 0.261 0.229 0.0129 -0.979 -0.1 -0.05 -0.1 -0.2 -0.05 -0.15 0 0 0 0 0 1;

0 -2.2477 -6.0221 -2.1794 -0.4907 -1.1498 -12.6899 0 0 0 0 0 0 0 0 0 0 0 0;

0 2.2477 6.0221 2.1794 0.4907 1.1498 12.6899 0 0 0 0 0 0 0 0 0 0 0 0;

0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0 0 0 0;

0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0 0 0;

0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0 0;

0 0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0 0;

0 0 0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0 0;

0 0 0 0 0 0 -1 0 0 0 0 0 KiFond 0 0 0 0 0 0]

b0=[-f1min/d1 -f2min/d2 -f3min/d3 -f4min/d4 -f5min/d5 -f6min/d6 0 0 0 0 0 0 -974600 1071840 -(1-Kizn+Kao)*Xot(1) -(1-Kizn+Kao)*Xot(2) -(1-Kizn+Kao)*Xot(3)...

-(1-Kizn+Kao)*Xot(4) -(1-Kizn+Kao)*Xot(5) -(1-Kizn+Kao)*Xot(6)]

Нижнюю - Xmin и верхнюю Xmax границы на переменные:

Kmin=1; Xmin = [Kmin*Xot Imin Yot]

Коэффициенты, определяющие развитие экономики региона:

KX=1; Kinv=0.05; KY=1;

Xmax = [KX*Xinv Kinv*Iinv KY*Ymax]

bl0 = [0.0 Xmin] %bl0=[0.0 88980 15277 28035 7336 72358 42136 0 0 0 0 0 0 35592 11757 22428 7116 36907 25275]

bu0 = [1.0 Xmax] %bu0=[1.0 97878 17000 31000 8500 79000 46000 17796 3055 5607 1467 14472 8427 39150 12933 24671 7827 40598 27803]

Исходные данные λ -задачи (40)-(50) используются при ее решении динамике на период планирования три года, ∆ t=1, 2, 3.(t⁰=2004 – этот го представлен отчетными данными Xmin).

Решение λ – задачи.

1 год планирования.

Решается задача на min.

[X01, L01]=linprog(-1*L, A0, b0, Aeq, beq, bl0, bu0);

X01 = 1.0e+004 0.0 9.2322 1.6772 2.9484 0.7973 7.5008 4.4304 0.0561 0.0075 0.0144.0036 0.0429 0.0223 3.6365 1.2495 2.3181 0.7425 3.7541 2.6003

L01 = 2.9791e-012

Решается задача на max (стандартным образом):

[X0, L0]=linprog(L, A0, b0, Aeq, beq, bl0, bu0);

В результате решения λ – задачи получили:

λ ^o =L0 = 0.7855 – оптимальный уровень (критерий);

X0 = [Lо = 0.7855 Xo = 94121 16013 29476 7770 76911 44809 Inv =890 153 280 73 724 421 Yo = 3.8387 1.2681 2.4190 0.7675 3.9806 2.7261] – Максимальная относительная оценка L0, валовой региональный продукт по каждой отрасли (верхняя строка) Xo={x_j, j= }, инвестиции - Inv и конечное использование (спрос) соответствующей отрасли (нижняя строка) y_j, j= .

Xo_Yo_Invs=[X0(2) X0(14) X0(8); X0(3) X0(15) X0(9); X0(4) X0(16) X0(10);

X0(5) X0(17) X0(11); X0(6) X0(18) X0(12); X0(7) X0(19) X0(13)]'

Xo_Yo_Invs = 94121 16013 29476 7770 76911 44809

38387 12681 24190 7675 39806 27261

890 153 280 73 724 421

Su_Xo1_Yo1_Inv =269100 150000 2540

279380 152980 2540

SuInvsMinMax = 1467.3 2541.2

Выполним проверку: l_k(X^o)=(f_k(X^o)-f )/(f -f ), k =

– оператор в системе Matlab примет вид:

Lymbda_Yo=[(X0(14)-f1min)/d1; (X0(15)-f2min)/d2; (X0(16)-f3min)/d3;

(X0(17)-f4min)/d4; (X0(18)-f5min)/d5; (X0(19)-f6min)/d6].

В результате решения получили:

l_k(X^o)= Lymbda_Yo = 0.7855 0.7855 0.7855 0.7855 0.7855 0.7855

этот вектор говорит о том, что в оптимальной точке X^o темп роста каждой отрасли достигает λ ^o = 0, 7855 от своей установленной величины, (которую определили заранее как 10% от отчетных данных).

Определим затраты ресурсов при таком выпуске отраслей -

Rtrud=-A0(13,:)*X0; dr1=b0(14)+ Rtrud;

RtrudX0_dR1=[-b0(13) Rtrud b0(14) dR1]:

Rtrud = 1033100– затраты ресурсов – количество человек необходимых для реализации взятых обязательств регионе;

dr1= 38739 – отклонения ресурсов от планируемого роста;

b0(14)=1071800 – планируемый максимальный рост трудовых ресурсов.

RtrudX0_dR1 = 974600 1033100 1071800 38700.

Темп роста каждой отрасли в системе Matlab определяется вектором:

Rost_Vid = [X0(14)/f1min; X0(15)/f2min; X0(16)/f3min; X0(17)/f4min; X0(18)/f5min;

X0(19)/f6min; (X0(2)+X0(3)+X0(4)+X0(5)+X0(6)+X0(7))/f7min;

(X0(14)+X0(15)+X0(16)+X0(17)+X0(18)+X0(19))/f8min],

который в числовом виде примет вид: Rost_Vid =[1.0785 1.0786 1.0786 1.0785 1.0786 1.0786 1.0589 1.0786].

На основе полученных объемов производства всех видов продукции X^o={X_j, j = }, используя коэффициенты матрицы валовой добавленной стоимости (ВДС) Z, рассчитаем:

оплату труда по каждому виду продукции региона Trud_Zp =[2.7955 0.3362 0.4009 0.0871 3.8158 1.8697];

налоговые отчисления по каждой отрасли: Nalog =[3618.1 1282.1 1126.8 222.8 4468.9 2472.0] (в т. ч. на федеральный, региональный и муниципальный уровни), - эти налоговые отчисления характеризуют налоговые поступления в доходную часть бюджета и являются стартовой точкой для расчета бюджета региона;

амортизационные отчисления: Amort =[7121 10 11 35 14632 8178];

прибыли фирм: Profit =[4900.7 76.5 93.6 62.5 3350.3 2824.5];

перечисленные денежные средства в совокупности представляют региональную валовую добавленную стоимость:

ValDobStoim = [43581 4714 5229 1191 60613 32176].

2 год планирования.

Рассматривается темп прироста трудовых ресурсов: temp=1.

Tzmin=temp*b0(13) = 984346 Tzmax=temp*b0(14)= 1082600

Полученные демографические показатели используются в векторе ограничений: b00 =-0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0 0 0 0 0 0 -984346 1082600 -89000 -15300 -28000 -7300 -72400 -42100

Полученные объемы выпуска отраслей - валовой региональный продукт x_j, j= и конечное использование (спрос) y_j, j= - используется как нижняя граница выпусков:

bl0=[0 88980 15277 28035 7336 72358 42136 0 0 0 0 0 0 35592 11757 22428 7116 36907 25275], а верхняя устанавливается на 10% больше - bu0 =[1 97878 17000 31000 8500 79000 46000 890 153 280 73 724 421 39150 12933 24671 7827 40598 2.7803]. В тестовом примере bl0 и bu0 не изменяется.

Выполняется расчет на 2-й год планирования.

[X0, L0]=linprog(L, A0, b0, Aeq, beq, bl0, bu0);

В результате решения λ – задачи на t=2 получили: оптимальную точку

X^o(2)=[ Lo = 0.8847 Xo =95003 16165 29754 7843 77628 45227 Inv =890 153 280 73 724 421 Yo =38740 12797 24412 7745 40172 27512]

L0 = -0.8847

Xo_Yo_Invs = 95003 16165 29754 7843 77628 45227

38740 12797 24412 7745 40172 27512

890 153 280 73 724 421

Su_Xo_Yo_Inv = 271620 151380 2540

27938 15298 254

Lymbda_Yo = 0.8847 0.8847 0.8847 0.8847 0.8847 0.8847

Rtrud = 1042800 dr1 = 29076

RtrudX0_dR1 = 974600 1042800 1071800 38700

Rost_Vid = 10884 10885 10885 10884 10885 10885 10688 10885

Полученные объемы производства всех видов продукции X^o={X_j, j= } служат основой расчета коэффициентов матрицы валовой добавленной стоимости (ВДС) Z на второй год планирования, аналогично как и на первый.

3 год планирования.

Рассматривается прирост трудовых ресурсов: Tzmin=994092, Tzmax=1093300.

Полученные демографические показатели используются в векторе ограничений: b00 =-0.0 -0.0 -0.0 -0.0 -0.0 -0.0 0 0 0 0 0 0 -994100 1093300 -89000 -15300 -28000 -7300 -72400 -42100

Полученные объемы выпуска отраслей - валовой региональный продукт x_j, j= и конечное использование (спрос) y_j, j= - используется как нижняя граница выпусков:

bl0=[0 88980 15277 28035 7336 72358 42136 0 0 0 0 0 0 35592 11757 22428 7116 36907 25275], а верхняя устанавливается на 10% больше - bu0 =[1 97878 17000 31000 8500 79000 46000 890 153 280 73 724 421 39150 12933 24671 7827 40598 2.7803]. В тестовом примере bl0 и bu0 не изменяется.

Выполняется расчет на 3-й год планирования.

[X0, L0]=linprog(L, A0, b0, Aeq, beq, bl0, bu0);

В результате решения λ – задачи на t=3 получили:

оптимальную точку X^o(3)=[Lo = 1 Xo =95613 16270 29946 7893 78124 45516 Inv =890 153 280 73 724 421 Yo =38984 12878 24566 7794 40425 27685], L0 = -0.9532

Xo_Yo_Invs = 95613 16270 29946 7893 78124 45516

38984 12878 24566 7794 40425 27685

890 53 280 73 724 421

Su_Xo_Yo_Inv = 27336 15233 254

27938 15298 254

Lymbda_Yo = 0.9532 0.9532 0.9532 0.9532 0.9532 0.9532

Rtrud = 1049400 dr1 = 22395

RtrudX0_dR1 = 974600 1049400 1071800 38700

Rost_Vid = 1.0953 1.0953 1.0953 1.0952 1.0953 1.0953 1.0757 1.0953

temp = 1.0300

Полученные объемы производства используются для расчета коэффициентов матрицы валовой добавленной стоимости (ВДС) Z на третий год планирования.

В целом результаты моделирования служат основой для различного вида финансовых задач и прежде всего для формирования бюджета региона.

Таким образом, математическая модель формирования развития региональной экономики дает возможность подсчитать валовые объемы и оптимальный темп роста экономики региона с учетом: во-первых, межотраслевого баланса, во-вторых, инвестиций вкладываемых в каждую отрасль региона, в-третьих, с учетом ресурсных возможностей региона и его производственных мощностей.

Таким образом, построенная модель и результаты моделирования могут служить основой для разработки экономической политики региона, то есть определяют линию поведения каждой отрасли (всех предприятий соответствующей отрасли).

Заключение. Анализ экономико-математических моделей региона показал, что моделирование, основанное на межотраслевом балансе и векторных оптимизационных моделях, позволяет исследовать отраслевые пропорции развития экономики края и учитывать межотраслевые взаимосвязи, возникающие вследствие обмена продукцией различных отраслей, формирование и распределение ресурсов определенных видов продукции, а также возможности и эффективность развития внешних связей.

[1] А. Файоль выделил пять элементов управления: предвидения, организации, распорядительство, координация и контроль, которые в дальнейшем названы функциями управления. [15].

[2] В работе специально включен фрагмент исходных данных из [3] с тем, чтобы показать переход от классического эконометрического построения функции спроса к оптимизационной модели, а в последующем к модели векторной.

[3] Норматив с 1 января 2009 года

[4] Норматив с 1 января 2009 года

[5] Органы государственной власти субъектов РФ обязаны установить единые и (или) дополнительные нормативы отчислений в местные бюджеты не менее 10% налоговых доходов консолидированного бюджета. (Практически это единственный налог, с помощью которого регион (субъект РФ) перераспределяет налоговые поступления между муниципальными образованиями внутри региона).

[6] Раздел написан совместно с И. А. Машуниным