
Главная страница
Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Билет 25.
1)Теорема Грина для многосвязной области. Пусть теперь D многосвязная на плоскости Oxy. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек. Рассмотрим случай, когда граница области D (на рисунке область заштрихована) состоит из внешнего контура С и внутренних контуров С 1 и С 2. Соединим контур С разрезом FM с контуром С 1, разрезом BG - с контуром С 2. (Под словами " соединим разрезом BG " подразумевается то, что мы удалим из D отрезок BG). Область 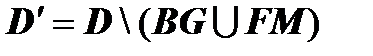 с границей с границей  односвязна, поэтому для неё справедлива формула Грина: односвязна, поэтому для неё справедлива формула Грина:
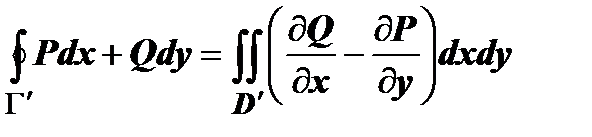 . Двойные интегралы по областям D и . Двойные интегралы по областям D и  равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой  интегралы по разрезам входят с противоположными знаками ( интегралы по разрезам входят с противоположными знаками ( и и  , например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей , например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей  . На множестве . На множестве  определены непрерывные функции определены непрерывные функции  и и  , имеющие непрерывные частные производные. Тогда , имеющие непрерывные частные производные. Тогда  , при этом каждая часть полной границы , при этом каждая часть полной границы  обходится так, что область D остаётся слева. обходится так, что область D остаётся слева.
2)
|

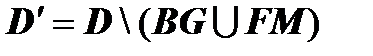 с границей
с границей  односвязна, поэтому для неё справедлива формула Грина:
односвязна, поэтому для неё справедлива формула Грина:
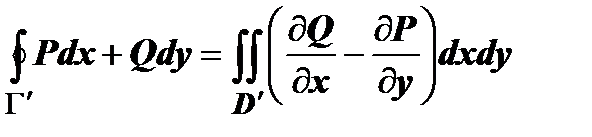 . Двойные интегралы по областям D и
. Двойные интегралы по областям D и  равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой
равны (площадь разрезов равна нулю); в криволинейный интеграл по кусочно-гладкой кривой  интегралы по разрезам входят с противоположными знаками (
интегралы по разрезам входят с противоположными знаками ( и
и  , например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей
, например) и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области: пусть на плоскости Oxy дана многосвязная область D с границей  . На множестве
. На множестве  определены непрерывные функции
определены непрерывные функции  и
и  , имеющие непрерывные частные производные. Тогда
, имеющие непрерывные частные производные. Тогда  , при этом каждая часть полной границы
, при этом каждая часть полной границы  обходится так, что область D остаётся слева.
обходится так, что область D остаётся слева.