Поверхностный интеграл второго рода (по координатам).

Определение поверхностного интеграла второго рода. Пусть в пространстве переменных x, y, z задана ограниченная кусочно-гладкая двусторонняя поверхность , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на 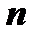частей , на каждой из частей выберем произвольную точку , найдём , нормаль в точке к выбранной стороне поверхности, и площадь проекции части на плоскость ОХУ. В интегральную сумму слагаемое возьмём со знаком " +", если (т.е. если угол между и осью Oz - острый; проекция на орт оси Oz положительна), и со знаком " -", если . В результате интегральная сумма будет иметь вид . Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения поверхности на части , ни от выбора точек , то функция R (x, y, z) называется интегрируемой по поверхности , а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается .

2). Векторные линии. Так как вектор (M) определяется длиной и направлением в пространстве, задание в области V поля (M) равносильно заданию в V полей длин и направлений. Геометрической характеристикой, определяющей в V поле направлений, служит совокупность векторных линий.

Определение. Векторной линией поля (M) называется любая линия, которая в каждой своей точке М касается вектора (M).

В силовой интерпретации поля векторными линиями являются силовые линии поля, в гидродинамической - векторные линии есть траектории, по которым движутся частицы жидкости (линии тока).

Получим дифференциальные уравнения векторных линий в декартовой системе координат. Пусть векторная линия определяется векторным уравнением . Тогда касательный вектор к этой линии в любой точке должен быть коллинеарен полю, т.е.

.

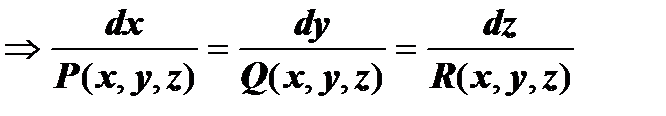Эта записанная в симметричной форме система из трёх уравнений первого порядка и определяет векторные линии. Так как функции P, Q, R одновременно не обращаются в нуль, то в любой точке одна из них отлична от нуля. Пусть, например, в точке . Тогда систему можно записать в виде . Функции P, Q, R непрерывно дифференцируемы, поэтому для последней системы выполняются условия теоремы существования и единственности задачи Коши с начальными условиями . Следовательно, через точку М ₀ проходит, и при том единственная, интегральная кривая системы, которая и будет векторной линией поля.

Пусть, например, поле . Тогда векторные линии определяются системой 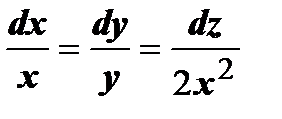. Решая уравнение , получим y = C ₁ x, из уравнения получаем 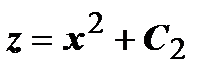, таким образом, уравнения векторных линий