
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Достаточные условия потенциальности.
|
|
Теорема. Если область V и поле  (M) удовлетворяют следующим условиям:
(M) удовлетворяют следующим условиям:
1. V - односвязная область;
2. Поле  (M) - безвихрево (т.е.
(M) - безвихрево (т.е.  ),
),
то  (M) - потенциальное в V поле.
(M) - потенциальное в V поле.
Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что  . Действительно, пусть
. Действительно, пусть 

|

|
| х |
| у |

|
| O |
| G |

|
| z |
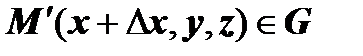 . Тогда
. Тогда  ,
,

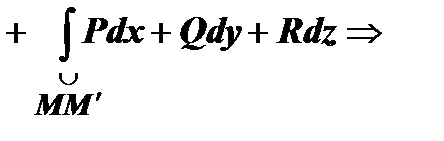
 (на
(на 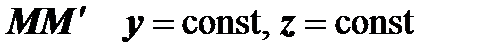 )
) 
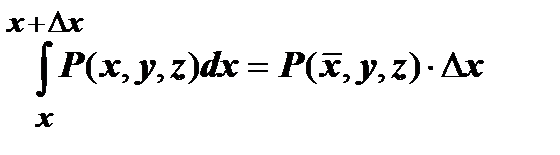 (по теореме о среднем)
(по теореме о среднем)  . Точка
. Точка  удовлетворяет условиям
удовлетворяет условиям  . Устремим
. Устремим  , тогда
, тогда  , и
, и  .
.
Аналогично доказывается, что  .
.
Задача 4.
Найдите площадь части поверхности сферы x2+y2+z2=a2, заключенной внутри цилиндра x2+y2=ax
Решение:
 .
.
z= √ (a2-(x2+y2))
z’x= - x/√ (a2-(x2+y2));
z’y= - y/√ (a2-(x2+y2));
s(σ) = ∫ ∫ √ (1+x2/(a2-(x2+y2))+y2/(a2-(x2+y2))) dxdy = a ∫ ∫ (1/√ (a2-(x2+y2))) dxdy = a ∫ dφ (пределы инт. От –π /2 до π /2) ∫ (1/√ (a2-r2)) dr(от 0 до a) = a ∫ dφ (пределы инт. От –π /2 до π /2) * arcsin(r/a) (от 0 до a) = aπ 2/2
Задача 5
Применяя формула Стокса, вычислите циркуляцию векторного поля a= (2x2 + 4z) i + (x-3y+z) j + (3y-2)k по контуру треугольника с вершинами A(0; 1; 0), B(0; 0; 1), C(1; 0; 1), обход совершается в направлении ABCA
Решение
Ц =  ;
;
n= {0; -1; -1};
n0 = 1/√ 2{0; -1; -1};
rot a = {2; -4; 1};
(rot a, n0) =3/√ 2
Ц= ∫ ∫ 3/√ 2 dS= 3/√ 2* SABC=3/√ 2*0.5*√ 2=1.5
Задача 6.
Исследуйте числовые ряды на сходимость
a)∑ (-1)n/(n- ln n) n=2….беск.
|an|= 1/(n- ln n) ̴ 1/n(1-ln n/n) ̴ 1/n, но по критерию сходимости Коши 1/n – гармонический расходящийся ряд => ряд расходится.
б) ∑ tg((-1)n+1π /2√ n) ̴ ∑ (-1)n+1π /2√ n;
|an|= π /2√ n= π /2n1/2< 1 => расходится