Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дивергенция векторного поля.
|
|
Пусть в некоторой системе координат 
. Скалярная величина (скалярное поле) 
называется дивергенцией поля в точке М и обозначается 
: 
. С помощью оператора набла дивергенция определяется как скалярное произведение 
. В дальнейшем мы увидем, что дивергенция инвариантна относительно системы координат и обозначает плотность источников поля, а сейчас сформулируем свойства дивергенции:
4. Если 
(M) - постоянное векторное поле, то 
;
5. 
(или 
);
6. Если u - скалярное поле, то 
(или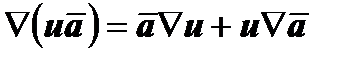 
). В частности, если (M) - постоянное векторное поле, то 
.
Докажем, например, третье свойство.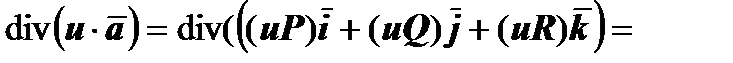 
.
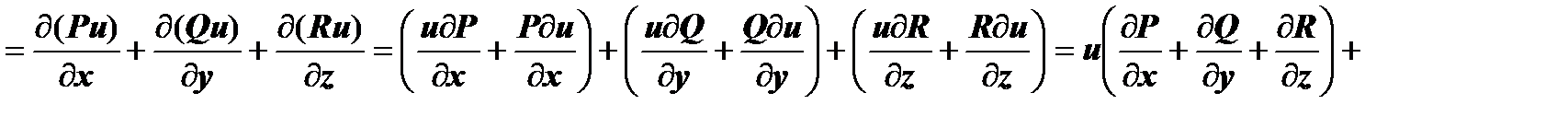
| M 1 |
| V |
|
| M |
. Теорема Остроградского позволяет понять смысл дивергенции поля в точке М как объективного атрибута векторного поля без использования координатной системы. Пусть - замкнутая поверхность, окружающая точку М, V - тело, заключенное внутри , 
- вектор единичной внешней нормали к . Тогда 
. По теореме о среднем для тройного интеграла существует точка 
такая, что 
. Следовательно, 
. Отношение значения некоторой физической величины к объёму принято называть средней плотностью этой величины в объёме; если объём стягивается к точке М, предел средней плотности называется локальным значением плотности в точке М. Таким образом, мы можем трактовать 
как среднюю плотность потока в объёме V. Будем теперь стягивать к точке М, при этом и V стягивается к точке М; 
, и, вследствие непрерывности 
, 
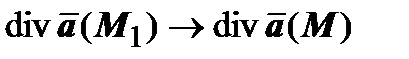. Поэтому 
будет равна плотности потока в точке М, и так как плотность потока определяется независимо от выбора какой-либо системы координат, то дивергенция векторного поля инвариантна относительно выбора координатной системы.
Используем теперь гидродинамическую интерпретацию поля для выяснения физического смысла дивергенции. Пусть (M) - стационарное поле скоростей несжимаемой жидкости. В каком случае поток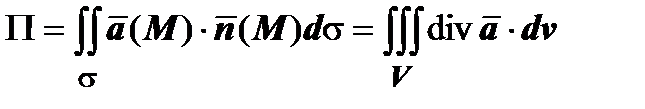 
через замкнутую поверхность может быть отличен от нуля, т.е. в каком случае из V вытекает больше жидкости, чем втекает (при П> 0) или наоборот (при П< 0)? Ясно, что П> 0 может быть только в том случае, если в V появляется дополнительная жидкость, т.е. в V имеются источники поля. П< 0 может быть только в том случае, если в V исчезает часть жидкости, т.е. в V имеются стоки поля. Поэтому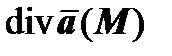 
как плотность потока в точке М определяет силу источника (при 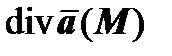> 0) или стока (при 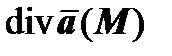< 0) в точке М.
По аналогии с полем скоростей жидкости считают, что дивергенция определяет силу источников и стоков поля в любом поле (M).