Теоремы об оценке интеграла.

1. Если функция интегрируема по области , и для выполняется , то .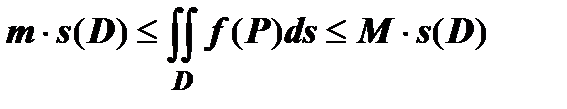

2. 2. Если функция интегрируема по области , то .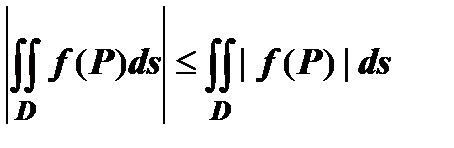

Теорема о среднем. Если функция непрерывна на области , то существует точка , такая что .

2) Пусть в некоторой системе координат . Скалярная величина (скалярное поле) называется дивергенцией поля в точке М и обозначается : . С помощью оператора набла дивергенция определяется как скалярное произведение .
свойства дивергенции:

1. Если (M) - постоянное векторное поле, то ;

2. (или );

3. Если u - скалярное поле, то (или 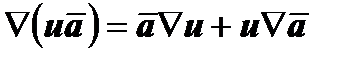). В частности, если (M) - постоянное векторное поле, то .

Признак сходимости Коши (радикальный). Пусть для положительного ряда существует . Тогда

если q < 1, то ряд сходится,

если q > 1, то ряд расходится,

если q =1, то ряд может и сходиться, и расходиться.

Доказательство. 1. Пусть < 1. Возьмём . .

Если q < 1, то число . Итак, при . Прогрессия сходится, так как р < 1, поэтому сходится, поэтому 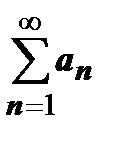сходится.

2. Пусть > 1. Возьмём . .

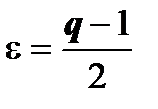Если q > 1, то число . Итак, при . Прогрессия расходится, так как р > 1, поэтому расходится, поэтому 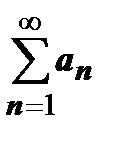расходится.

3. Чтобы убедиться, что в случае q =1 мы не можем сделать вывод ни о сходимости, ни о расходимости ряда, рассмотрим два примера: и . Первый из этих рядов сходится, второй расходится, но в обоих случаях q =1, например .

4)Вычислить объем тела ограниченного поверхностями x^2+y^2+z^2=0, z=0, x+y+z=5.

Решение:

x^2+y^2+2z=0 - цилиндр

z=o плоскость
x+y+z=5 - плоскость

=

= =2+pi/2

5) a=(2x-y+2z)i-(x+2y-z)j+(3z-2y)k

По контотуру треугольника АВС: А(2, 2, 0) В(0, 0, 3) С(3, 0, 1)

Решение:
AB(-2, -2, 3), BC(3, 0, -2)
найдем нормаль к плоскости:

n= = 4i+5j+6k

n₀ =

6) f(x)=

Ряды фурье!!