
Главная страница
Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Билет 19
1) Область V- простая (правильной), если выполняются два условия: проекция V на какую-либо координатную плоскость простая область D, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку V, пересекает границу V в двух точках.
Теорема о переходе от тройного интеграла к повторному. Если V - простая область с кусочно-гладкой границей, f(x, y, z) - непрерывная функция, то  . .
Доказ. Установим, что для повторного интеграла в правой части формулы имеют место все свойства интеграла, разбьём область V на подобласти Vi (i=1, 2…n), пользуюсь свойствами аддитивности и теоремой о среднем, представим повторный интеграл как интегральную сумму для тройного ⎟  и перейдём к пределу при d=max diam(Vi) → 0. и перейдём к пределу при d=max diam(Vi) → 0.
Распишем двойной интеграл по простой области D  в виде повторного, получим формулу для вычисления тройного интеграла: в виде повторного, получим формулу для вычисления тройного интеграла: 
Пример.  V-внутренность конуса. D-проекция окружности на уровне z=h на Оxy. V-внутренность конуса. D-проекция окружности на уровне z=h на Оxy.  . .
2) Определение поверхностного интеграла второго рода. Пусть в пространстве переменных x, y, z задана ограниченная кусочно-гладкая двусторонняя поверхность  , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке  задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на 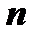 частей частей  , на каждой из частей , на каждой из частей  выберем произвольную точку выберем произвольную точку  , найдём , найдём  , нормаль , нормаль  в точке в точке  к выбранной стороне поверхности, и площадь к выбранной стороне поверхности, и площадь  проекции части проекции части  на плоскость ОХУ. В интегральную сумму слагаемое на плоскость ОХУ. В интегральную сумму слагаемое  возьмём со знаком " +", если возьмём со знаком " +", если  (т.е. если угол (т.е. если угол  между между  и осью Oz - острый; проекция и осью Oz - острый; проекция  на орт на орт  оси Oz положительна), и со знаком " -", если оси Oz положительна), и со знаком " -", если  . В результате интегральная сумма будет иметь вид . В результате интегральная сумма будет иметь вид  . Если существует предел последовательности интегральных сумм при . Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения поверхности , не зависящий ни от способа разбиения поверхности  на части на части  , ни от выбора точек , ни от выбора точек  , то функция R (x, y, z) называется интегрируемой по поверхности , то функция R (x, y, z) называется интегрируемой по поверхности  , а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается , а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается  . Обычно рассматривается сумма этих интегралов, которая обозначается . Обычно рассматривается сумма этих интегралов, которая обозначается 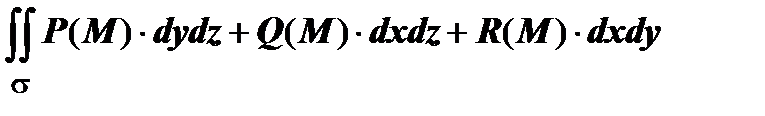 . .
Физический смысл: поток векторного поля  через поверхность через поверхность  в направлении внешней нормали.(сколько жидкости протекает за единицу времени через заданную поверхность). в направлении внешней нормали.(сколько жидкости протекает за единицу времени через заданную поверхность). 
Пример. Вычислить  , где s - часть плоскости , где s - часть плоскости 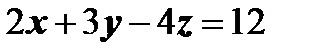 , ограниченная координатными плоскостями x =0, у =0, z =0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz. , ограниченная координатными плоскостями x =0, у =0, z =0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
Решение. Из двух направлений нормали к s  мы должны выбрать такое, для которого коэффициент при орте мы должны выбрать такое, для которого коэффициент при орте  (т.е. (т.е.  ) положителен, поэтому выбираем знак " -", тогда ) положителен, поэтому выбираем знак " -", тогда  . В соответствии со знаками направляющих косинусов, . В соответствии со знаками направляющих косинусов, 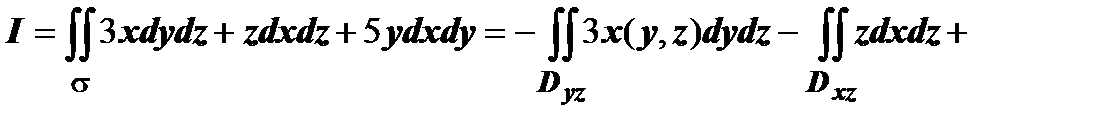 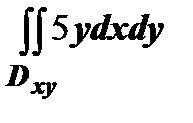 . Вычисляем эти интегралы. . Вычисляем эти интегралы.
1.   . .
2.  . .
3.   . Окончательно, . Окончательно, 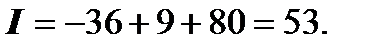
3) Интегральный признак Коши. Док-во условия сходимости рядов Дирихле.
Теорема. Пусть члены положительного числового ряда  являются значениями непрерывной монотонно убывающей неотрицательной функции являются значениями непрерывной монотонно убывающей неотрицательной функции 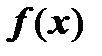 при натуральных значениях аргумента: при натуральных значениях аргумента:  Тогда ряд Тогда ряд  и несобственный интеграл и несобственный интеграл  сходятся или расходятся одновременно. сходятся или расходятся одновременно.
Теперь мы можем дать простое доказательство того, что ряд Дирихле 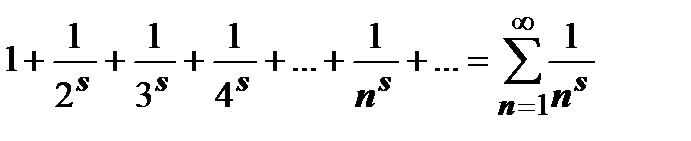 сходится при s > 1 и расходится в остальных случаях. Функция сходится при s > 1 и расходится в остальных случаях. Функция  удовлетворяет условиям теоремы: непрерывна, монотонно убывает, удовлетворяет условиям теоремы: непрерывна, монотонно убывает,  . Интеграл . Интеграл 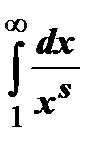 сходится при s > 1 и расходится при других значениях s. сходится при s > 1 и расходится при других значениях s.
4)  
5)   
Промежуточная точка С(π /2; -π /4) 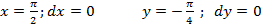
I)  II) II)  dx=1 Конечный ответ I=2 dx=1 Конечный ответ I=2
6)   
 x(-∞; +∞) x(-∞; +∞)
|

 .
. и перейдём к пределу при d=max diam(Vi) → 0.
и перейдём к пределу при d=max diam(Vi) → 0. в виде повторного, получим формулу для вычисления тройного интеграла:
в виде повторного, получим формулу для вычисления тройного интеграла: 
 V-внутренность конуса. D-проекция окружности на уровне z=h на Оxy.
V-внутренность конуса. D-проекция окружности на уровне z=h на Оxy.  .
.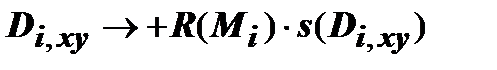







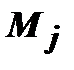



 , на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке
, на которой введена ориентация (т.е. с помощью единичного вектора нормали в какой-либо точке  задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на
задана сторона поверхности), и на которой определена функция R (x, y, z).Разобьём поверхность на 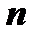 частей
частей  , на каждой из частей
, на каждой из частей  выберем произвольную точку
выберем произвольную точку  , найдём
, найдём  , нормаль
, нормаль  в точке
в точке  к выбранной стороне поверхности, и площадь
к выбранной стороне поверхности, и площадь  проекции части
проекции части  на плоскость ОХУ. В интегральную сумму слагаемое
на плоскость ОХУ. В интегральную сумму слагаемое  возьмём со знаком " +", если
возьмём со знаком " +", если  (т.е. если угол
(т.е. если угол  между
между  и осью Oz - острый; проекция
и осью Oz - острый; проекция  на орт
на орт  оси Oz положительна), и со знаком " -", если
оси Oz положительна), и со знаком " -", если  . В результате интегральная сумма будет иметь вид
. В результате интегральная сумма будет иметь вид  . Если существует предел последовательности интегральных сумм при
. Если существует предел последовательности интегральных сумм при  , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности  на части
на части  , ни от выбора точек
, ни от выбора точек  , то функция R (x, y, z) называется интегрируемой по поверхности
, то функция R (x, y, z) называется интегрируемой по поверхности  , а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается
, а значение этого предела называется поверхностным интегралом второго рода, или поверхностным интегралом по координатам х, у, и обозначается  . Обычно рассматривается сумма этих интегралов, которая обозначается
. Обычно рассматривается сумма этих интегралов, которая обозначается 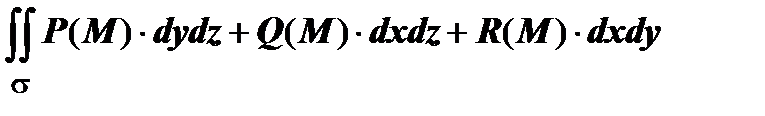 .
.  через поверхность
через поверхность  в направлении внешней нормали.(сколько жидкости протекает за единицу времени через заданную поверхность).
в направлении внешней нормали.(сколько жидкости протекает за единицу времени через заданную поверхность). 
 , где s - часть плоскости
, где s - часть плоскости 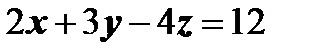 , ограниченная координатными плоскостями x =0, у =0, z =0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz.
, ограниченная координатными плоскостями x =0, у =0, z =0. Сторона поверхности выбирается так, чтобы нормаль образовывала острый угол с осью Oz. мы должны выбрать такое, для которого коэффициент при орте
мы должны выбрать такое, для которого коэффициент при орте  (т.е.
(т.е.  ) положителен, поэтому выбираем знак " -", тогда
) положителен, поэтому выбираем знак " -", тогда  . В соответствии со знаками направляющих косинусов,
. В соответствии со знаками направляющих косинусов, 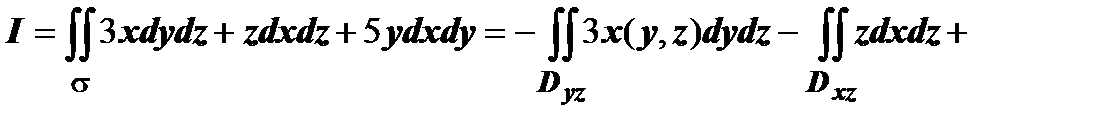
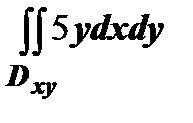 . Вычисляем эти интегралы.
. Вычисляем эти интегралы.
 .
.
 .
.

 . Окончательно,
. Окончательно, 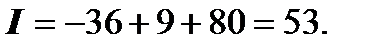
 являются значениями непрерывной монотонно убывающей неотрицательной функции
являются значениями непрерывной монотонно убывающей неотрицательной функции 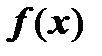 при натуральных значениях аргумента:
при натуральных значениях аргумента:  Тогда ряд
Тогда ряд  и несобственный интеграл
и несобственный интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.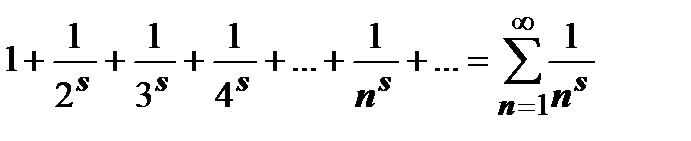 сходится при s > 1 и расходится в остальных случаях. Функция
сходится при s > 1 и расходится в остальных случаях. Функция  удовлетворяет условиям теоремы: непрерывна, монотонно убывает,
удовлетворяет условиям теоремы: непрерывна, монотонно убывает,  . Интеграл
. Интеграл 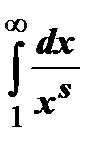 сходится при s > 1 и расходится при других значениях s.
сходится при s > 1 и расходится при других значениях s.




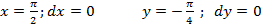
 II)
II)  dx=1 Конечный ответ I=2
dx=1 Конечный ответ I=2


 x(-∞; +∞)
x(-∞; +∞)