
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Билет №16. 1. Выпишите формулы для вычисления моментов инерции неоднородных тел.
|
|
Приведите примеры. (6 баллов)
Плоские тела
m=  - масса 2-ного объекта - масса 2-ного объекта
 = =  – момент инерции относительно оси OX; – момент инерции относительно оси OX;
 = =  – момент инерции относительно оси OY; – момент инерции относительно оси OY;
 = =  = =  + +  – полярный момент инерции. – полярный момент инерции.
| Объемные тела
m=  -масса 3-ного объекта -масса 3-ного объекта
 = =  – момент инерции относительно плоскости XOY; – момент инерции относительно плоскости XOY;
 = =  – момент инерции относительно плоскости XOZ; – момент инерции относительно плоскости XOZ;
 = =  – момент инерции относительно плоскости YOZ; – момент инерции относительно плоскости YOZ;
 = = 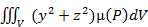 – момент инерции относительно оси OX; – момент инерции относительно оси OX;
 = =  – момент инерции относительно оси OY; – момент инерции относительно оси OY;
 = =  – момент инерции относительно оси OZ; – момент инерции относительно оси OZ;
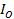 =ng w: val=" EN-US" /> < /w: rPr> < m: t> P< /m: t> < /m: r> < /m: e> < /m: d> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: lang w: val=" EN-US" /> < /w: rPr> < m: t> dV< /m: t> < /m: r> < /m: e> < /m: nary> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> =ng w: val=" EN-US" /> < /w: rPr> < m: t> P< /m: t> < /m: r> < /m: e> < /m: d> < m: r> < w: rPr> < w: rFonts w: ascii=" Cambria Math" w: fareast=" Times New Roman" w: h-ansi=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: i/> < w: lang w: val=" EN-US" /> < /w: rPr> < m: t> dV< /m: t> < /m: r> < /m: e> < /m: nary> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> ">  – полярный момент инерции. – полярный момент инерции.
|
Пример. Найти  неоднородной пластины, ограниченной кривыми
неоднородной пластины, ограниченной кривыми
 . Если плотность µ(x, y)=y+1.
. Если плотность µ(x, y)=y+1.
Решение:
 =
=  =2
=2  =
=  .
.
2. Докажите, что в потенциальном поле криволинейный интеграл не зависит от пути интегрирования. Формула Ньютона-Лейбница. (6 баллов)
Определение: Векторное поле называется потенциальным, если существует такая функция u(M), что выполняется равенство a(M) = grad (u(M)).
a(M) =P(x, y, z) i +Q(x, y, z) j +R(x, y, z) k;
Значит P(x, y, z)=  Q(x, y, z)=
Q(x, y, z)=  R(x, y, z)=
R(x, y, z)= 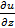
 =
=  =
=  =u(B)-u(A).
=u(B)-u(A).
Теорема: Если в односвязной области G значение криволинейного интеграла не зависит от пути интегрирования, то выполняется условие 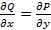 .
.
Теорема: Если в односвязной области G выполнено условие 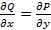 , то существует функция u(x, y) такая, что для любых точек A(
, то существует функция u(x, y) такая, что для любых точек A( €G и В(
€G и В( ) €G.
) €G.
 =u(
=u( -u(
-u( .
.
Функцию u(x, y) принято называть потенциальной функцией.
Доказательство:

Фиксируем точку  (
( ). Скажем что u(x, y)=
). Скажем что u(x, y)=  . Тогда
. Тогда 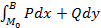 =
=  +
+  =>
=>  =
= 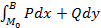 -
-  =
=  -
-  =u(B)-u(a). Это обобщение формулы Ньютона-Лейбница на 2-ный случай.
=u(B)-u(a). Это обобщение формулы Ньютона-Лейбница на 2-ный случай.